《1 前言》

1 前言

自 19 世纪 40 年代《南京条约》签订，以上海为代表的第一批通商口岸被迫开放以来，上海作为我国对外贸易往来的重要交通枢纽为众人所熟知。特别是 19 世纪 70 年代，伴随着黄浦江和苏州河两岸近代工业集聚区的兴起，上海逐步奠定了其东方航运中心的地位。新中国成立后，借助于上海市及长江三角洲的紧密联系，通过临港工业的互动、国际航运中心建设的持续推动，上海港保持着上升的发展势头，维持着其强有力的竞争优势。

然而，在发展过程中，上海港及临港产业正遭遇发展空间不足的瓶颈。

首先，在有限的地理维度中，上海和长江口深水岸线及土地已经达到了近乎饱和的状态。具体而言，目前上海港主力港区分布于外高桥、洋山、罗泾，而临港产业主要集中在江口南岸、杭州湾金山、临港新城及长江口长兴岛南岸。因而，重新寻找到完整的深水岸线及近岸土地已然成为制约发展的难题。

其次，上海港集装箱码头和散杂货码头的能力已趋超负荷。以外高桥港区为例，2011年外高桥港区集装箱吞吐量已是设计能力的1.39倍，而洋山港区吞吐量也已达到了设计能力的 1.41 倍。有研究推算，上海港需要维持每年 2×106 ~3×106 TEU 增量才能达到长江流域对外贸易发展的需求，而临港临海可用工业岸线土地资源已无法满足。

再者，上海港作为建设中的国际航运中心，功能尚未完善，尤其水水中转能力较弱。目前部分集装箱的水水中转功能主要由洋山港兼顾，大宗散货的中转均有罗泾港区和外高桥港区兼顾，但受各港区自身的条件限制，中转能力较弱（特别是与长江流域各港口），无法使上海港成为完善的综合运输枢纽。

最后，上海周边大型港口不断崛起，上海国际航运中心的龙头地位受到严峻挑战。例如与邻近的舟山港相比较，2011 年，上海港包括内河在内的全港货物吞吐量达到7.27×108 t，而宁波—舟山港为 6.94×108 t，当年两港增速分别为11.4 %和12 %，从增速看，势均力敌。但2012年，宁波—舟山港增速快速领先上海港，达到7.2 %，远超上海港的1.1 %，同时宁波—舟山港货物吞吐量达到7.44×108 t，首次突破7×108 t，超过上海港800余万吨，从而将上海港从雄踞多年的货物吞吐量全球第一的位置上挑落下马。从集装箱增量看，2012年，上海港比2011年增加7.9×105 TEU，而宁波—舟山增量为9.8×105 TEU，此项上也是首次超过上海港。综上所述，上海港面临的问题集中在上海土地、岸线、航道等资源后备严重不足，制约了上海港及临港产业发展空间及布局。在此港口资源发展壁垒的情况下，横沙东滩的开发可谓是应运而生。

第一，横沙东滩近期可提供的土地为1.7×105 亩（1亩≈666.67 m2 大一区范围），全部成陆后总共成陆的面积约5.8×105 亩，可形成的岸线总长在90 km以上，并且可利用直接面向外海的有利条件，采用大型挖入式港池等手段，增加深水岸线，解决了上海港所无法满足的土地和深水岸线资源的问题。

第二，横沙东滩自身拥有非常好的优势，作为长江出海口的桥头堡，可满足江海联运的紧迫要求。一方面，横沙东滩通江达海，具有良好的地理位置。它位于长江出海口，扼守我国海岸线与长江黄金水道的T字形交点，若与长兴岛（海洋装备岛）用短距离隧道或桥梁连通后，即可经沪崇苏陆上通道直抵上海浦东和苏北。此外，横沙东滩与洋山深水港水域距离约100多千米，与外高桥港区（南港南岸）水域距离约30千米。借助其地理优势，可逐渐形成上海国际航运中心的港口群，确立“横沙港— 洋山深水港—南港”三足鼎立的格局，达到功能互补合理分配资源的目的。

另一方面，横沙东滩可挖掘潜力大。第一，横沙东滩已批准促淤圈围的面积为112 km2（1.7×105 亩，大一区）。在其东侧还约有 270 km2（4.1×105 亩）的滩涂存在，可作为中远期促淤圈围规划。第二，横沙东滩北侧有50 km以上岸线资源、紧贴北港航道，其中约14 km为目前10 m以深的深水岸线，其余为目前 7 m 左右深水岸线；南侧约 48 km 岸线紧邻长江口北槽 12.5 m 航道。随着北港航道整治规划实施，岸线水深将不断增加，存在巨大的开发潜力，东部及东侧亦可形成连接深水15~20 m的大型港池或人工岛。第三，航道资源丰富。横沙东滩地处横沙岛，南贴长江口北槽深水航道，北靠北港航道，西接长江黄金水道，东临东海。长江口深水航道10 m水深已向上贯通到南京长江大桥，2010年3月长江口的航道已达到12.5 m水深，并将逐步向上延伸到南京长江大桥。北港航道规划为10 m航道。横沙通道水深维持 10 m。第四，有效可利用泥沙资源充足。长江口丰水丰沙，大通站多年的年平均输沙量为4.08×108 t，近年来下泄泥量虽有所减少，但也有上亿吨的泥沙下泄，长江口口门地区的滩涂淤涨能力依然较强。第五，成陆速度快。在横沙东滩南侧，长江口深水航道的年疏浚维护量可达 7×107 ~ 8×107 m3 ；在横沙东滩北侧，北港航道已在筹备建设，届时也将产生大量的疏浚土。这些疏浚土就近吹填上滩，即可加快横沙东滩的成陆过程，也可减少航道疏浚土的二次回淤现象，实现资源综合利用。

因此，开发横沙东滩，建设海港物流中心，完善国际航运中心功能成为迫在眉睫的发展需要。从近期看，开发横沙东滩，形成新港区及临港产业区（长江桥头堡海港物流中心及临海产业），与外高桥、洋山形成新的航运中心格局；从长远看，横沙东滩、九段沙、南汇边滩这些长江口门区域的大片滩涂可综合起来，形成陈吉余院士提出的长江口亚三角洲，建设上海真正的港口群及海洋经济带。

综上，为了配合上海国际航运中心的建设，利用长江流域的疏浚土在横沙岛吹填土地，建立新的港口或将成为一条非常行之有效的道路。那么将面临的数学问题就是，如何将长江口岸的淤泥（图1 中两条深色部分）吹填到它们所夹的粗线所围区域内，使得总工程耗费最少。

《图1》

图1 横沙东滩及长江口淤泥示意图

Fig.1 East Hengsha shoal and the schematic diagram of silt at Yangtze River estuary

《2 数学模型》

2 数学模型

将这个问题转化为一个数学模型，就是困扰数学家 232 年的世界难题——“Monge-Kantorovich问题”。

1781 年，Monge G 提出了最优输运问题（即 Monge 问题）[1] ：假如要挖一个给定形状的土坑，搬到另一处堆出一个给定形状的建筑物，怎样运土可以使所作的功达到最小[2] ，如图2所示。

《图2》

图2 Monge问题背景

Fig.2 Monge problem background

这个问题在一维的情况下早已经解决。如果要把x 处的土搬到处，记为x 处的深度， p（y）为 y 处的设计高度，那么最优的方案是是满足的单调递增函数。但是在平面上的问题就要远远复杂了。主要原因是在平面上没有像直线上的线性关系。

下面用数学语言把Monge问题重述如下：一个可分度量空间U，V上的测度μ、v 和一个单位费用函数C（x，y），同时记

问题转化为：寻找一个变换T0∈Γ1使得

其中，T0为最优映射，I （T0）为最优运输费用。

通常单位费用函数 C（x，y）是非负的下半连续函数，常见的有：

线性费用：C（x，y）= |x - y | ；

平方费用：C（x，y）= |x - y | 2 ；

L p 费用：C（x，y）= |x - y |p ,p ∈(1,+∞) ；

C（x，y）= ϕ (|x - y |) ，ϕ 为某一凸函数。

其中|x - y |表示x、y 之间的直线距离，Monge最初研究的是线性费用情况。

自从Monge问题问世以来，它就成为了数学中几个领域的数学家们所共同关心的经典主题。微分几何学家 Appell P 在 1887 年发表了一篇非常精彩的文章建立了一些最优映射在平面和 R3 中的几何性质[3] 。但由于 Monge 问题的不适定性，即使在一般欧式空间中，其最优输运映射的存在性问题也不是那么显而易见的。

为了解决这个困难，在 1924 年 Kantorovich 提出了输运问题的弱解形式[4] ，Kantorovich 当时并不知道Monge的工作。Kantorovich 问题简述为：找到 U×V 上的概率测度 γ0 ∈Γ={在 U×V 上边际分布为 μ。v 的概率测度全体}，使得：

他的本质思想就是去寻找方案而不是输运弱解，也就是说，去寻找空间U×V 中的概率测定，而不是两个空间之间的映射。在两者之间的联系中，可以注意到，任意的输运映射T 都可以推出一个方案 γ，这个方案重点关注T 在x×y 中的图谱，而且很容易证明反之亦成立。由于上述原因，任何一个输运都可以推出一个具有相同成本的方案这就导致了

因此，所有的Γ内的极值点都是由输运推导而来的，那么可以直接从 Kantorovich 格式中得出输运映射的存在性。 Kantorovich 格式可以看成是原来Monge问题的一个弱解形式。

至此，人们将上述最优输运问题统称为 “Monge-Kantorovich 输运问题”，该问题又引发了学术界更多的关注，Kantorovich 与他的学生 Rubinstein 得到了著名的对偶公式[5，6] ，将“Monge-Kantorovich 问题”很好地引入了经济学、自动化控制、运输学、流体力学、几何学、形状优化、气象学和金融数学等众多领域。1991 年Brenier Y用凸函数的梯度刻画了最优映射[7] ，他的这篇文章建立了最优输运问题与偏微分方程、概率论与泛函分析间的美妙联系。从此最优输运问题变得极其流行，应用非常广泛。

目前，这个问题的一维情况已经被广泛研究[2，8] ，但是二维情况直到三年前才被郑伟安和他的博士生沈银芳所解决[9] ，该文的想法是把原来的问题化为下列的二阶拟线性椭圆偏微分方程的边值问题。

这里未知函数 u 是一个二维的概率分布函数， ux 与 uy 分别是 u 对 x 与对 y 的偏导数。藉此可以简单地算出最佳的平方距离E |X -Y |2 ，它的平方根给出 Monge 原问题的一个均方意义下的解。用此可以估算出原问题中欲求的“功”。

对这个数学问题感兴趣的读者可以参考陈木法院士的文章[10] .

《3 数学证明的简述》

3 数学证明的简述

根据Kantorovich的表述，只需要找到两个随机的向量X=（X1，X2）与Y =（Y1，Y2），满足下列条件：

1）X 具有概率密度函数 q（x1，x2），Y 具有概率密度函数p（y1，y2）；

2）E |X -Y |2 是所有满足上述条件的随机向量对中最小的。

文献[9]中的想法是，假定（X，Y）就是欲找的最佳的一对。可以构造新的随机变量Z=（X1，X2）。于是

有趣的是，此时X 与Z 只有一个分量不同，Z 与 Y 也只有一个分量不同。如果知道Z 的密度函数，则根据前述的一维解法，X 与Z 的关系就固定了，同理Z 与Y 的关系也固定了。于是问题简化为求Z 的密度函数。更进一步，如果Z 的概率分布函数知道了，那它对体积的导数就是Z 的密度函数，所以问题又进一步简化为求Z 的概率分布函数u 如下。

实际上，E |X -Z  |2 与E |Z -Y  |2 都可以用一个含有 u 的积分式表示出来。所以用数学中常用的变分法就可以从（5）得到（4）。

《4 数值模拟算法及结果》

4 数值模拟算法及结果

本文用文献[9]中的结论作为求解的依据再加上线性规划的思想来模拟计算工程量。在设计算法时，首先将要求解的区域分成若干个小正方形单元，如图3所示，图中共划分了20×30个单元，每个小正方形单元的边长对应实际情况中的2 km。划分好网格后，将该实际问题转化为可求解的数学模型，如图4所示。

《图3》

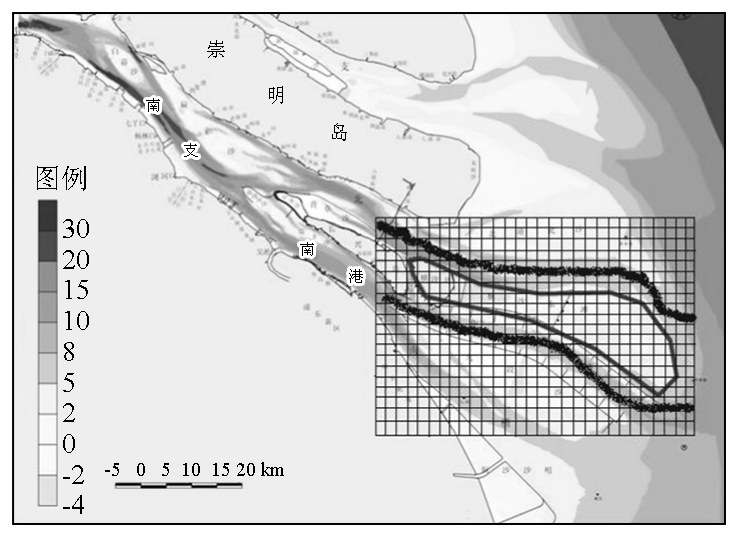
图3 区域网格划分

Fig.3 Mesh plots of the region

《图4》

图4 数学模型示意图

Fig.4 Schematic diagram of the mathematical model

设计算法如下：

1）用常用的线性规划寻找每一大块（4 km2 的方格）搬运的最优方案；

2）在每个对应的小单元中，用前面所述的 “Monge-Kantorovich 输运问题”解法分析每块淤泥填到既定目标区的均方意义下的功。

线性规划问题：初始给定两个矩阵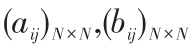的最优化问题可以化为

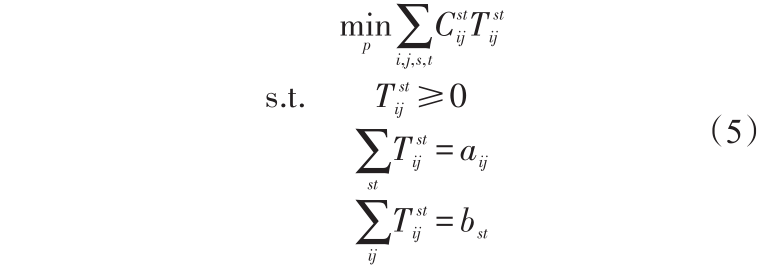
式中，表示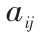的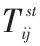部分移动到了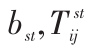的花费为。

其拉格朗日函数为：

由于问题的数据量较大，通过 KKT 条件直接求解矩阵的逆，计算量会很大。因此使用交替方向法[11] 和并行运算，求解该极小化问题：

初始化 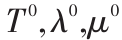，选取步长 h

取 k =1,2,3,⋯

计算｛

取 j =1,2,3,⋯

分块计算｛

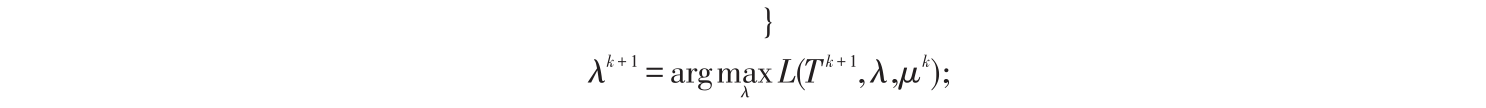
更新：

而在每个对应的小单元中，计算文献[9]中的给出的变分问题：

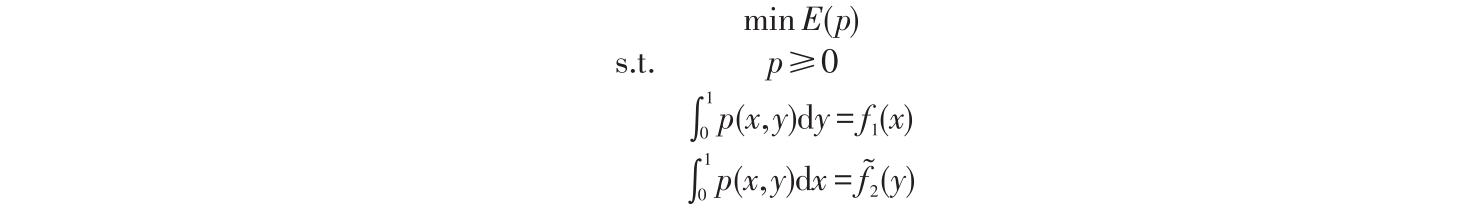
其中

等价于求解极小化问题：

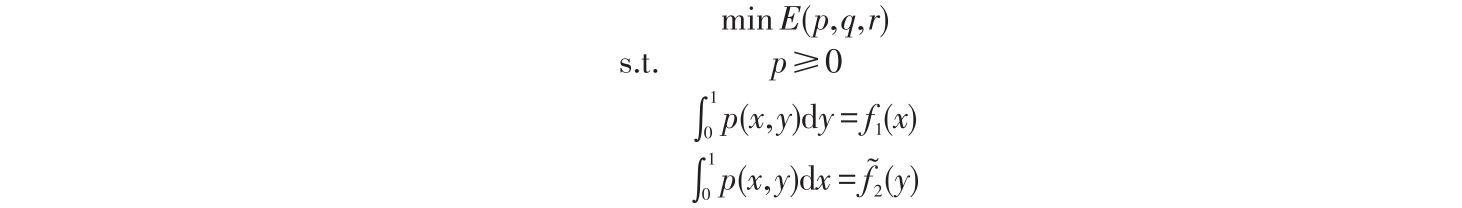
其中

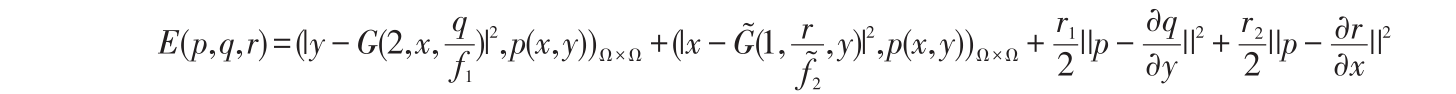
是常数。

使用交替下降法等计算方法，求解该变分问题的最优值。算法如下：

初始化；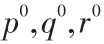

取 k =1,2,3,⋯

当

计算｛

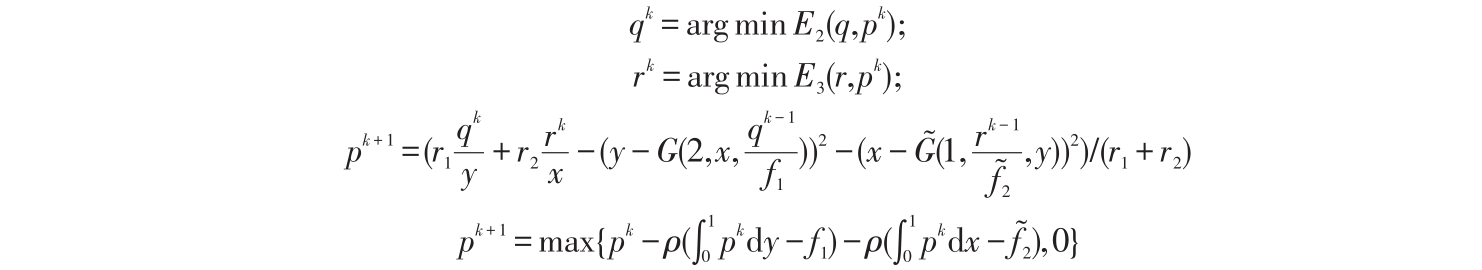
更新： k =k +1.

在假设每平方千米单位深度的水里有公斤泥沙，每顿泥沙搬运一千米需要b 元的情况下，用上述算法初步估计出工程总耗为22 000元。当然这是在没有任何水文资料与实际工程制约情况下的简单估算，实际问题难得多。

《5 模型的扩展》

5 模型的扩展

由于长江口的淤泥是随着时间不断增长的，而且还受到台风的影响，所以在实际应用中会有更多的难度。因为这个问题还牵涉到了随时间的变换。由于挖泥的形状和次序影响以后新淤泥的堆积，目前还无法把它化为一个精确的数学题。但是可以从下列偏微分方程根据历史数据确定悬浮泥沙的浓度。

式中，S 为悬浮沙的浓度；u、v、w 为x、y、z 方向的流体速度；Kh 、Kv 为水平与竖直方向的扩散系数；Ws 为泥沙沉降速度。

《6 结语》

6 结语

随着上海国际航运中心的龙头地位日益面临严峻挑战，为了配合上海国际航运中心的建设，利用长江口流域的疏浚土在横沙岛吹填土地，建立新的港区或将成为一条非常行之有效的道路。本文以长江口疏浚土吹填横沙东滩为背景，将其转化为数学模型：“Monge-Kantorovich 输运问题”，以此设计算法，进而得到最有运输条件下的总工程耗费。由于工程本身的规模巨大，通过寻找最优的输运方案，能够最大限度地减少施工费用支出，降低工程造价成本。为了更好地模拟实际操作过程中所可能遇到的问题，全文最后还讨论了模型进一步的扩展提升，提出了可将其转化为一个与时间变化有关的问题，以加强模型的适用性。