《1 前言》

1 前言

多孔材料广泛存在于自然界，并在日常生活和工业生产中起着非常重要的作用[1~4]。 例如，人们从很早以前就使用泡沫材料来保护精密设备和仪器免受猛烈碰撞。材料的多孔特性能够极大地改变其动力学与热力学特征。当物体受到弱冲击作用时，其中空隙的存在可能使两碰撞物体出现二次碰撞；当冲击作用较强时，材料内部空隙处可能会出现射流[2,4]；在张力波作用下材料内空隙的集结控制着材料的破碎方式[5]；在多孔炸药中，空隙特征对起爆所需的冲击阈值具有决定性影响[4]。以前的相关研究主要集中在冲击 Hugoniots[6]和状态方程[7]。然而，在冲击加载和卸载过程中，多孔材料中会出现复杂的时空耗散结构，系统整体处于极度的非平衡状态。对这种非平衡过程动力学和热力学的研究还非常薄弱。在文章中，引入积分几何和数值图像处理中的 Minkowski 泛函[8]来处理系统热力学特征量例如温度的 Turing 斑图， 揭示出 3 个 Minkowski 泛函（白色区域相对面积、边界总长度、欧拉特征量）与系统中“高温区”所占份额、“热点”在空间的分布方式之间的对应，揭示出 Minkowski 泛函演化特征与冲击波与多孔材料相互作用过程之间的对应。

在冲击波作用下多孔材料的响应过程涉及到大变形和很强的非线性，其理论描述非常复杂，所以除实验外，这方面的研究（特别是一些快速过程的再现和细节研究）在很大程度上依赖于数值模拟。从模拟方面来说，分子动力学可以揭示出空隙塌缩的一些微观机制[9,10]，但其所涉及的时间和空间尺度尚局限在纳秒和几十纳米量级，远不能满足实验要求。对于这类涉及到材料大变形的问题，纯拉氏和纯欧氏算法均遇到了一些不易克服的困难：拉氏方法能够很好地跟踪物质的界面，但在处理大变形时会遇到网格畸变的问题；在欧氏方法中，网格不随物体的变形而变化，但是它不易跟踪物质的界面。为充分发挥欧氏和拉氏算法的优点、避免其缺点，笔者等将使用最近发展起来的一种混合方法──物质点法来模拟多孔材料的冲击动力学与热力学。

《2 多孔材料的物理模型》

2 多孔材料的物理模型

在模拟系统中，多孔材料的初态是由一块完整的固体内嵌一定数量的空隙来构成。固体材料特性用带线性硬化的 von Mises 塑性模型来描述[4]。塑性模型是指在屈服条件满足之前材料表现出线弹性响应。von Mises 屈服判据为 3J2 - Y2＝0，其中 Y 是塑性屈服应力，J2 是偏应力张量 s（＝ σ -Tｒ［σ］/3）的第二不变量。线性硬化是指 Y 随着塑性应变张量的第二不变量线性增加。当 3J2 ＞ Y2 时，等效塑性应变增量 dεp 可 以 按 下 述 方 式 计 算： dεp 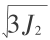＝（ －Y） ／（3G ＋ Etan ） ，其中 G 和 Etan 是剪切和硬化模量。 塑形能增量 dWp ＝ dεp · Y 全部转化为内能。压力 p 满足 Mie－Gruneissen 状态方程

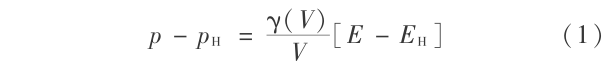
式中 pH ，VH 和 EH 为 Rankine - Hugoniot 曲线上的压力，比容和内能。pH 和 VH 之间的关系如下：

其中 c0 是声速；λ是 Hugoniot 线性关系 Us ＝c0 ＋λUp 中的系数；Us 和 Up 是冲击波速和波后粒子速度。在文章中，Gruneissen 系数 γ（VH）取为常数，比内能 E - EH （VH）取为塑性功，暂时不考虑热耗散。冲击压缩和塑性功都导致温度的升高。冲击压缩导致的温升为

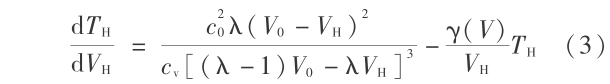
其中 cv 是比热。塑性功导致的温升为

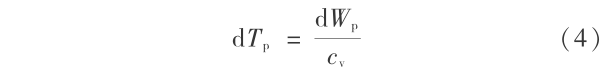
材料参数如下：密度 ρ0 ＝2700 kg/m3；弹性模量 E = 69 GPa；泊松比 ν = 0.33；初始屈服应力为 σ0 = 120 MPa；硬化模量 Etan =384 MPa； 声速 c0 = 5.35 km/s；热容量 cv = 880 J/(kg· K)， 热传导系数 k = 237 W/(m · K) 。在模拟过程中，冲击波的加载通过多孔材料本身和静止在 y = 0 处的固壁碰撞来实现。 多孔材料位于固壁的上方。在 t = 0 时刻以速度 -vinit 与固壁开始碰撞。在水平方向使用周期边界条件，这样，一个模拟单元的结果恰好对应于由许多完全一样的模拟单元沿水平方向并列摆布而构成的较大系统的情形。在文章中，集中考虑二维问题。初始温度取为 300 K 。

《3 形态学量度与热力学特征的对应》

3 形态学量度与热力学特征的对应

冲击作用下多孔材料中各状态量呈现出复杂的时空分布，可以采用一系列统计手段对其进行处理和分析。文章中引入和使用的是积分几何和数值图像处理中的 Minkowski 泛函[8,11]，又称为形态学量度。

如果给所描述的物理量设置一个阈值，高于该阈值的区域定义为白色，反之定义为黑色，那么几乎所有的连续图案都可以分解为一些白色和黑色像素组成的小尺度斑图。Minkowski 泛函（Minkowski 量度或形态学描述）为这类 Turing 斑图提供了一套完备描述。在 d 维空间中，这些 Minkowski 泛函的个数为 d +1 。在二维情形，这 3 个 Minkowski 量度分别对应于白色区域的总面积、链接黑白区域的边界总长度和 Euler 特征系数，其中 Euler 特征系数又称为链接度。这 3 个 Minkowski 量度具有可加性、运动不变性和连续性特征。由于实验设备精度的限制或者由于计算机模拟的内禀的离散特征，在很多时候人们所获得的图形表现为一个由一系列像素组成的结构，所以，形态学描述可以在许多物理过程的分析中起到非常大的帮助作用。

如果需要处理和分析的是一幅温度分布图，那么上述白色区域对应于“高温区域”，黑色区域对应于“低温区域”，那些零星的白色像素或斑图可以视为材料中出现的“热点”。下面就简单叙述这 3 个量度的具体计算与性质。描述物理场形态学特征的第一 Minkowski 量度为白色面积 A，定义为温度 T 高于阈值 Tth 的像素的个数 NW 与总像素数目 N 之比，即 A = NW /N 。当阈值 Tth 从温度的最小值变化到最大值时，白色面积 A 从 1 逐渐减小到 0 。第二量度为边界长度 L，定义为链接白色区域和黑色区域的边界总长度 B 与像素总数目 N 之比，即 L = B/N。当阈值 Tth 从温度的最小值变化到最大值时，边界长度 L 从 0 开始增加；当 Tth 取某一值的时候，达到最大值；然后逐渐下降到 0 。第 3 个量度 Euler 特征系数 χ 定义为 χ＝（nW - nB ) /N ，其中 nW（nB）为链接在一起的白色（黑色）区域的个数。与白色面积 A 和边界长度 L 不同，Euler 特征系数 χ 从纯拓扑的角度来描述图案特征。它描述的是白色和黑色区域的联通性。当未连接在一块的黑色区域的数目多时，χ< 0 ；反之 χ> 0 。尽管描述的是整体特征，但也可以通过一些局域的方式来计算。

《4 物质点法的基本思路》

4 物质点法的基本思路

该方法由流体力学的 PIC 发展而来。 其中，连续物体被离散成 Np 个离散的拉格朗日质点，每个质点携带有质量 mp ，应力 σp ，速度 v ，密度 ρp 等信息；背景网格采用欧拉法描述，网格结点 i 携带有速度  vi  和加速度 ai 的信息。在每一个时间步，将物质点 p 携带的物质信息映射到背景网格结点 i，在背景网格节点 i 上求解动量方程，获得网格节点的速度、加速度；然后再映射回物质点处，更新下一时刻物质点所携带的物质信息。在每一个时间步均采用原始背景网格，因此避免了因网格畸变而产生的数值困难。下面简要地叙述其基本原理：

在物质点法中，每个物质点的质量不随时间变化，所以质量连续性方程

自动满足，其中 ρ 代表密度，v 代表速度。拉氏力学平衡方程为：

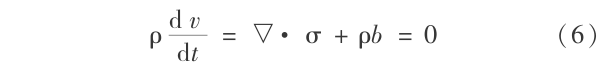
其中 b 代表体力。在每个时间步，物质点的质量和速度被映射到背景网格节点上。节点速度通过下式得到：

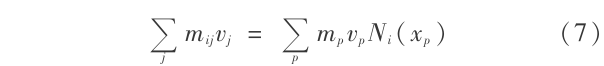
其中 Ni 是单元形函数，xp 代表物质点 p 的位置。当物质点的质量、速度信息映射到背景网格节点上后，方程（6）的弱形式就可以得到了：

其中 Ω 代表求解域，Γt 代表力边界，t 代表外力。由于连续体被离散成一系列的物质点，密度可以表示为：

把方程（9）带入（8）就可以把积分方程转化为在所有物质点上的求和：

其中，（fi）int 和（fi ）ext 分别代表外部力和内部力向量。

式（11）中，向量（fi）ｃ 代表接触力以及外部边界力。采用显式时间积分来求解式（10）可以得到节点加速度。物质点方法的核心为接触算法的构造。笔者等采用的是近期改进的接触算法[4]。

《5 数值模拟结果与分析》

5 数值模拟结果与分析

在笔者等的模拟中，多孔材料单元高 5 mm 宽 1 mm 。由于在水平方向使用周期边界条件，模拟结果也适用于由这样一些材料单元在水平方向相继排列而构成的较宽的多孔物体。图 1 给出孔隙度 δ = 1.7，初始碰撞速度 vinit = 1000 m/s，在时刻 t = 500 ns 的位型温度和位型压强图。图中的长度单位为 μm，上图中的颜色分布对应于温度，下图中的颜色描述的是压强。温度的单位是 K，压强的单位是GPa 。显然，与密实材料情形不同，温度、压强等物理量在空间的分布极不均匀。下面使用 3 个 Minkowski 量度对这一过程进行刻画和描述，并且从中提取与密实材料情形非常不同的一些物理信息和规律。

《图1》

图1 多孔材料在冲击波作用下的位型温度（上）和位型压强（下）图

（t ＝500 ns，长度单位为 μm）

Fig.1 Configurations with temperature （upper） and pressure （lower） of porous material under shock（t ＝500 ns and the length unit is μm）

温度 Turing 图的 Minkowski 描述如图 2 所示。图例中的 DT 代表 Tth = T -300 。 例如 DT = 10 意味着 Tth = 310 K 。当阈值温度为 310 K 时，高温区域的面积 A 随时间从 0 增加，到 1400 ns 时增加到 1，这一结果维持到 2300 ns，然后开始下降。这说明：a. 部分前期压缩波在 1400 ns 左右到达上自由表面，然后部分稀疏波开始返回； b. 在加载过程中，几乎所有被压缩波扫过区域的温度皆在 310 K 以上。当阈值温度 Tth = 400 K 时，高温面积 A 先是随时间迅速增加，到 1350 ns 时增加出现慢化，到 2350 ns 时达到最大值 0.993 。与 Tth = 310 K 时的情况相比较，可以获得如下信息：在多孔材料中，温度的升高是有个过程的；在整个过程中总有少许（高于 0.7 %）物质粒子不能达到 400 K 。这反映了如下基本图像：当原来的冲击波在传播过程遇到空隙时，空隙会反射回稀疏波；同时，如果有射流产生，那么射流物质撞击下游壁时产生新的冲击波；如果没有射流产生，则空隙两侧的压缩波会以相对较快的速度通过。这一过程在多孔材料的下游区域将反复出现。这样，原来的冲击波在传播过程中被逐渐分解为一系列压缩波和稀疏波，这些压缩波和稀疏波之间在时间上存在一系列相位差，即压缩波到达上自由表面的时间存在先后次序。每次压缩和塑性做功导致一次温度升高。当温度阈值 Tth = 500 K 时高温面积进一步减小，在整个过程中的最大值为0.954；在从 1950 ns 到 2500 ns 的时间区间内，95 % 左右物质粒子的温度在 500 K 以上；当 t ＝3000 ns 时，温度在 500 K 以上的面积减小至92 % 。从 DT = 250 的 A（t）曲线可以看出，在 t ＝ 2500 ns 时，温度高于 550 K 的面积达到最大值 0.90，到 t ＝3000 ns 时温度高于 550 K 的面积降至 88.6 % 。在图中所示的时间尺度内，温度阈值为 600 K，650 K，700 K 和 800 K 的 A（t） 曲线一直在上升。在 t ＝3000 ns 时，到达温度 600 K，650 K，700 K和 800 Ｋ的物质粒子数分别为 73 %，42 %，16 % 和 2 % 。这再次说明，多孔材料中的物质粒子可能依次接受多次压缩波作用。

《图2》

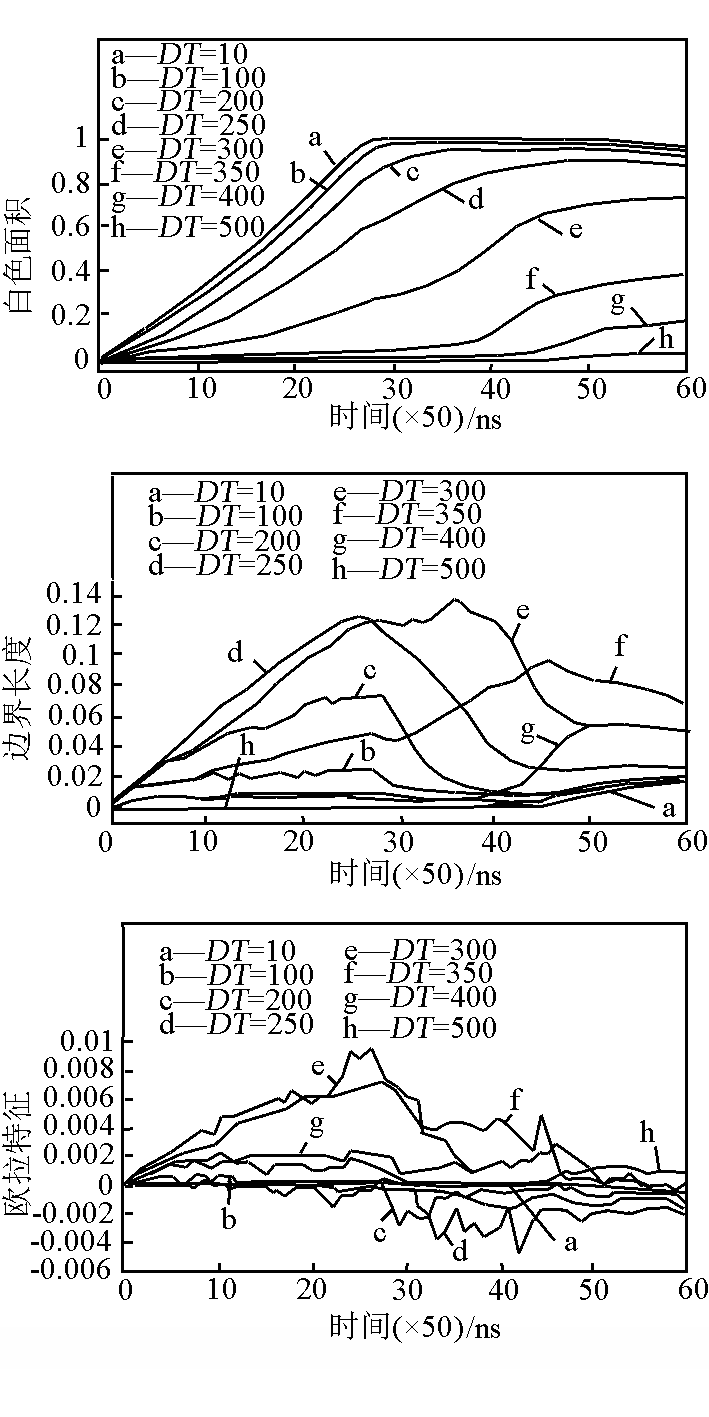
图2 温度 Turing 图的 Minkowski 描述（δ ＝1.7）

Fig.2 Minkowski description of the Turing patterns for temperature（Here δ ＝1.7）

下面来看边界长度 L ( t）曲线提供的信息。可以看到，DT ＝10 对应的边界长度随着碰撞开始迅速达到 0.005，然后随时间缓慢线性增加，到 1250 ns 时达到最大值 0.0076，到 1400 ns 时减小到约等于 0；2300 ns ＜ t ＜ 2800 ns 为 L（t）迅速增长时间，然后从 L ＝0.0156 开始震荡式缓慢衰减。 从整体来看，DT ＝10 对应的边界长度很小，在压缩波加载过程中近似为常数。这说明，在 DT ＝10 对应的温度 Turing 图上，压缩波扫过的区域为高温区，反之为低温区；压缩波波前近似为一平面，这一平面随时间向前推进，直到上自由表面。在这批压缩波达到上自由表面的瞬间，整块多孔材料的温度均在 310 K 以上，故 L（t）减小至 0 。2300 ns ＜ t ＜ 2800 ns 期间 L（t）的迅速增长是由于稀疏波的介入，上自由表面附近开始出现温度低于 310 K 的物质粒子，对应于白色面积的轻微减小。当温度阈值提升到 400 K 时，L（t）需要更长的时间增长到最大值 0.0247，这段时间对应于白色面积的增长期间；然后迅速下降到 0.0133，这一迅速下降对应这批压缩波到达上自由表面，稀疏波由上自由表面返回；接下来的是一段相对缓慢的下降，这对应于白色面积的缓慢增加，并且说明：白色面积的增加主要是由原来未连接在一起的一些零散的“热点”合并而导致的；当白色面积由最大值开始下降时，L（t）再次迅速增加，说明原来连载一起的“高温区域”开始离解为分散的“热点”。当温度阈值进一步提升到 500 K，550 K 和 600 K 时，L（t）的最大值逐渐增大；当提升到 650 K，700 K 和 800 K 时，L（t）的最大值逐渐减小。

第 3 重要的量度为 Euler 特征系数，即连通度。在冲击加载过程中，Tth ＝ 310 K 对应的 χ 值一直近似为 0，这与前面的分析是一致的：整个温度 Turing 图可以看作是一白一黑两个区域。在卸载过程中，χ 值向负的方向偏移，对应温度 Turing 图中出现的离散的“低温点”。在冲击加载过程中，Tth ＝ 400 K 对应的 χ 值一直略大于 0，这说明压缩波扫过区域出现了一些离散分布的“热点”。当 Tth = 500 K 时，在加载过程中，除了最初的接触碰撞阶段外， χ 值由正变负，说明温度 Turing 图由分散的高温区域数目占优势变化到分散的低温区域数目占优势。当 Tth 提升到 550 K 时，边界长度的增加导致几乎相等数目的白色、黑色区域的出现，白色区域的个数略多。当 Tth 取为 600 K 或 650 K 时，边界长度的增加使得白色区域的数目更加占优势。由于在这一冲击条件下，只是在后期，当部分稀疏波已反射回多孔介质后，温度达到 700 K，800 K 的物质粒子数才明显大于 0，所以在白色面积约等于 0 的过程中，略大于 0 的 χ 值对应于零星的非常小的“热点”。

接下来，使用 Minkowski 泛函考察不同冲击强度的效应。由于随着冲击速度的降低，系统的温升幅度迅速减小，所以笔者等选择较低的温升阈值（DT ＝10）进行比较。图 3 给出了初始碰撞速度分别为 300 m/s，500 m/s，800 m/s 和 1000 m/s 情形下的 Minkowski 泛函随时间的演化规律。随着碰撞速度的增加，白色面积随时间的增长速率增加，由近线性过渡到近抛物型。 冲击速度越大，压缩波的传播速度越大，多孔效应越显著。关于边界总长度 L（t）和 Euler 特征系数 χ（t） 的演化曲线可以按前面的方式进行理解。

《图3》

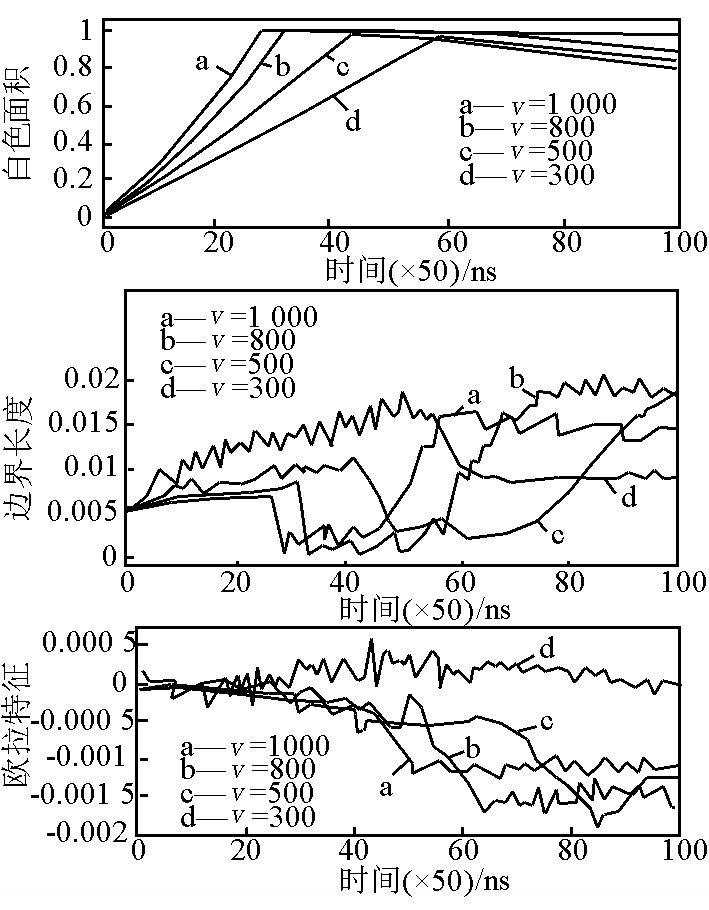
图3 不同冲击强度条件下温度 Turing 图的 Minkowski 描述（DT ＝10）

Fig.3 Minkowski description of Turing patterns for temperature under various shock strength（DT ＝10）

最后，考察材料空隙度的效应。图 4 给出了不同孔隙度条件下 DT ＝10 对应的温度 Turing 图的 Minkowski 描述。孔隙度数值 1.05，1.1，1.4，1.7 和 2 标注在图例中。这里初始撞击速度 vinit ＝ 500 m/s 。由 A（t）图可见，随着孔隙度的递增，白色面积趋于 1 的速率下降，即响应压缩波的传播速度降低。在图 4 所示的几种情形，δ ＝ 1.05 对应的边界长度 L（t）最大、 χ（t） 值最小（绝对值最大）。这说明在温度 Turing 图 中，多个小的黑色区域（T ＜ 310 K）的点缀在白色背景中。当 DT 提升到 20 时，仍是 δ ＝ 1.05 对应的边界长度 L（t） 最大、χ（t） 值最小（绝对值最大）；但 δ ＝ 1.05 时的白色面积 A（t）在加载过程中只增加到了 73 %；在随后 A（t）的减小过程中，边界长度 L（t）逐渐达到最大。当 δ ＝ 1.4，1.7 和 2 时，在加载过程中，边界长度 L（t）很小，同时白色面积 A（t）稳步提高，见图 5 。随着 DT 的进一步提升，低孔隙度情形所能达到的白色面积份额逐渐减小。当 DT ＝ 30，40，50 时，δ ＝ 1.1 对应的边界长度 L（t）在加载过程中最大，见图 6 。

《图4》

图4 不同孔隙度条件下温度 Turing 图的 Minkowski 描述（DT ＝10）

Fig.4 Minkowski decription of Turing patterns for temperature under various porosities（DT ＝10）

《图5》

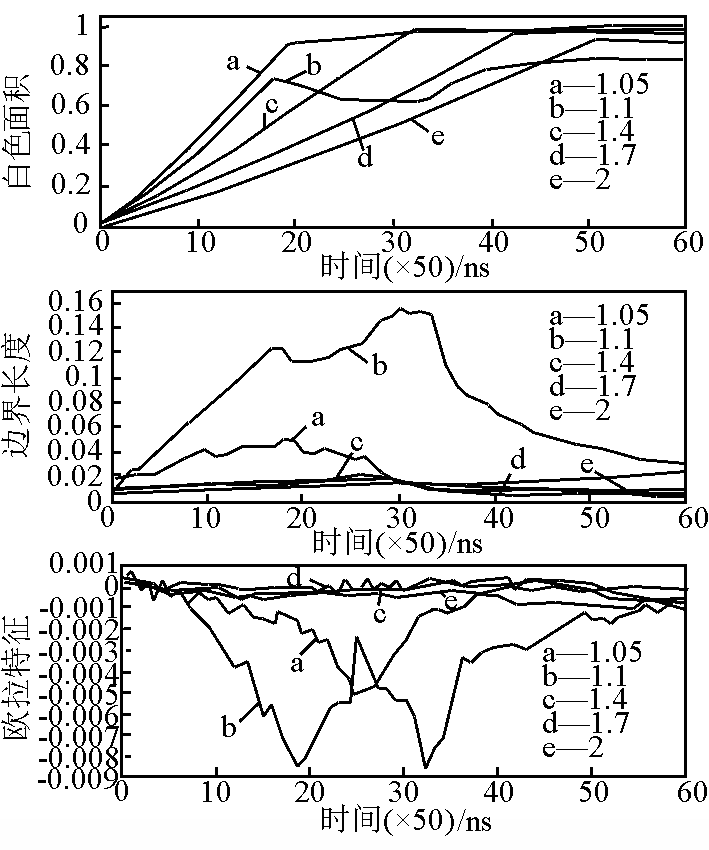
图5 不同孔隙度条件下温度 Turing 图的 Minkowski 描述（DT ＝20）

Fig.5 Minkowski description of Turing patterns for temperature under various porosities （DT ＝20）

《图6》

图6 不同孔隙度条件下温度 Turing 图的 Minkowski 描述（DT ＝50）

Fig.6 Minkowski description of Turing patterns for temperature under various porosities（DT ＝50）

《6 结语》

6 结语

使用物质点方法对冲击波与多孔材料的相互作用过程进行直接模拟， 对多孔金属材料中出现的复杂时空耗散结构引入形态学描述，揭示出 3 个 Minkowski 泛函（白色区域相对面积、边界总长度、Euler 特征系数）与系统中“高温区”所占份额、“热点”在空间的分布方式之间的对应，揭示出 Minkowski 泛函演化特征与冲击波及多孔材料相互作用过程之间的对应。 进一步发现，在多孔材料中的冲击加载表现为一些列压缩波与稀疏波的依次作用；不同温升阈值条件下，白色面积的增长速率是不同的；压缩波在多孔介质中的传播速度随孔隙度的提高而降低；冲击波越强，多孔效应越显著。