《1 引言》
1 引言
人工智能是诞生于20世纪50年代的新兴学科, 经历了50多年的时间, 已显示出其蓬勃的发展能力和广阔的应用前景。人工智能研究的目的是用机器模拟人脑的思维。目前大致可分为三个学派:符号学派、联结学派和行为学派, 各自通过不同的途径来实现机器的智能。人类的思维是多样性的, 很多思维现象体现为对确定性信息的处理, 而更多的现象却体现了各种各样的不确定性。这些不确定性包括模糊性、不精确性、不完整性、可变化性等等。因此, 人工智能系统应能很好反映人脑思维的不确定性, 并对各种不确定性信息进行处理。
集合论是诞生于19世纪末的一门学科, 发展到今天, 它一方面奠定了数学大厦的基础, 另一方面也有了很大的扩展, 产生了包括模糊集、可拓集、粗糙集、Vague集合、集对分析、FHW (模糊灰色物元空间) 、FEEC (模糊可拓经济控制) 等多种新型的集合论。每一种新集合论的产生都为人类思维的一种不确定性的描述提供了很好的手段, 并为人工智能处理一类不确定性信息提供了很好的方法。例如, 模糊集描述了思维的模糊性;可拓集描述了思维的可拓性;粗糙集描述了思维的不精确性等等。而经典集合恰恰描述了人们确定性思维。可以说, 一种集合论对应着人类的一种思维方法。
人类思维的基础体现在对一个事物的认识上, 这种认识又体现在对任意一个事物的隶属上, 而隶属这个概念正是各种集合论所研究的核心问题。综合各种集合论思想, 不难发现一些共同的性质。因此, 有必要站在历史的高度综合研究各种集合论, 从而诞生了初步的统一集论。
《2 统一集以及相关的概念》
2 统一集以及相关的概念
《2.1统一集及其表示》
2.1统一集及其表示
人类思维认识的本质体现在事物与概念之间的隶属上。为了描述这种隶属关系, 首先, 需要确定一个讨论的范围;其次, 对讨论范围内的任何一个事物都定义一个很好的描述, 描述的全体一般构成了概念的集合;第三, 这些描述可能还要受到一些限制。因此, 统一集定义为
《图1》
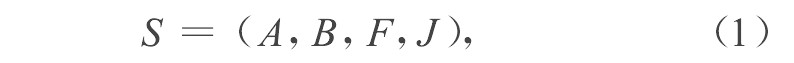
其中:S是一个统一集;A是一个非空的经典集合, 定义所要讨论的事物范围;B 是一个非空的经典集合, 对A中所有元素的描述构成集合;F是一个A到B的映射, 它给A中所有的元素都定义了描述;J是一个对F构成约束的界壳
在这个模型中, 为了对集合A中的元素进行描述, 选择了另一个集合B。一般情况下, B选择的都是性质较熟悉的集合。F构成了对A的描述, 虽然对F的约束可以写到映射F中, 但这里把约束独立出来作为统一集的一个要素J。
在统一集中, 一个元素和它的描述是分不开的。因此, A中的任意一个元素a都可以表示成二元组的形式:
《图2》
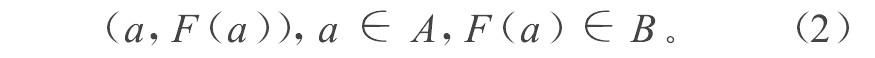
这里, F (a) 被认为是一种广义的隶属度;F被看成一种广义的隶属函数。A中的所有元素都可以用上面的二元组表示。因此, 统一集S还可以表示为
《2.2统一集的扩展》
2.2统一集的扩展
在式 (2) 中, a表示为A中的一个元素, 它可以是一个数、一个事物, 也可以是一个集合, 同样, a也可以是一个统一集或若干统一集的组合。同理, F (a) 也可以是一个统一集或若干统一集的组合。当元素a或F (a) 是统一集或组合时称S为一个被扩展的统一集。有了扩展, 使统一集模型的表达能力更加丰富。统一集S1中的任意一个元素S2也可以是统一集, 而S2中的元素S3又可以是一个统一集……。这样就有了统一集的嵌套, 把嵌套的深度定义为统一集的阶。
一阶统一集的具体例子:
其中 a = (A2, B2, F2, J2) 是一个统一集。
如果用约束界壳J表示集合, 那么这个集合可以是经典集合或模糊集合等等, 也可以用统一集的形式来表示, 但是, 统一集的阶与J无关。
《2.3统一集与各种集合论》
2.3统一集与各种集合论
有了统一集的模型, 可以用一种统一的形式来表达其他各种各样的集合, 并包容多种理论。
《2.3.1 普通统一集》
2.3.1 普通统一集
0阶扩展统一集称为普通统一集。在普通统一集中, 集合中的元素是基本的, 经典集合、模糊集合、可拓集合、Vague集合、FHW、FEEC等都可以认为是普通的统一集。
1) 经典集合[2]
其中A=U为经典集合的论域, C (x) 为特征函数, B是{0, 1}, 约束为空集∅。
2) 模糊集合[3]
其中A=U是模糊集合的论域, μ (x) 是隶属函数, 它描述U中任意一个元素隶属于一个模糊概念的程度, B为[0, 1], 约束为空集∅。
3) 可拓集合[4]
是为了描述人类思维中的可拓性也就是可变化性、可拓展性的集合论。综合物元分析可拓论有望模拟人类的创造性思维。
其中:A=U是可拓集合的论域, k (x) 是关联函数, 它描述U中的任意一个元素的可拓程度, B为实数域, 约束为空集∅。
4) Vague集合[5]
Vague集合是从Fuzzy集合中直接扩展出来的, 它弥补了传统Fuzzy集合的只能描述事物正隶属度的不足, 而是从隶属于一个概念的真假两个方面来考虑。用统一集可以把Vague集合表示为
其中: U是Vague集合的论域, B是单位正方形, F是由t (x) 和f (x) 表示的一个对子, t (x) 表示真隶属度, f (x) 表示假隶属度, t (x) 和f (x) 满足约束t (x) +f (x) =1, 这个约束写入界壳J中。
5) 模糊灰色物元空间 (FHW) [6]
FHW是一套用于宏观复杂大系统的决策支持系统, 它融合了模糊数学、可拓学、灰色系统、思维科学等多种学科, 曾在长江三峡的决策中产生了很好的实际应用效果。在FHW对方案进行评比选优时, 每一个方案都可以用一组模糊集合来对这个方案从当前、潜在、优劣度等多个方面进行评价。一个FHW空间用统一集的形式表示为
《图3》
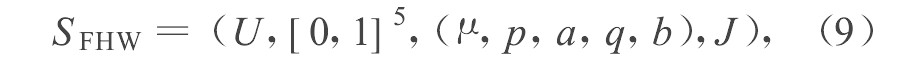
其中:A=U是论域包含了所有的待评价的方案, F是一个五元组, 其中任何一个元素都是U上的函数, B是一个五维的单位超立方体, (μ, p, a, q, b, ) 分别表示U中元素的总体评价、当前的优度、潜在的优度、当前的劣度、潜在的劣度, 这些参数既反映了评价方案的当前的优劣度又反映了潜在的、未来的优劣, 因而它对方案的评价更加科学;决策问题受到的约束为J。映射中的每一个参数都是一个模糊隶属度, 这些参数的获得都是综合了Delphi决策方法, 由若干个专家打分并进行最后综合而得来。
6) 模糊可拓经济控制 (FEEC) [7]
FEEC是一种模糊可拓经济控制的方法, 它结合了可拓学、模糊控制技术、集对分析和其他一些最新系统科学理论, 将经济系统看作一个开放的宏观复杂大系统, 运用从定性到定量综合集成法进行经济分析和控制研究。进行系统分析时, 首先要建立一个模糊可拓经济空间 (FEES) , 它用统一集的形式表示为
任何一个经济实体都可以用它的实力状态和虚力状态表示, 要研究的是在约束J下对实力和虚力进行转换。FEEC研究经济系统的特点是利用模糊数学、可拓学、集对分析、混沌学、灰色系统以及基于Fuzzy方法的软科学决策支持系统等最先进的理论, 建立一种定性与定量综合的控制方法。
《2.3.2 一阶统一集》
2.3.2 一阶统一集
在一阶统一集中, 任何一个统一集的元素仍然都是一个统一集。
1) 集对分析[8]。
集对分析是通过比较两个集合所构成集对的同、异、反三个方面, 为集对进行定性与定量相结合的描述。如果考虑两个论域中所有可能的集对, 可以用统一集来描述这些集对类:
《图4》
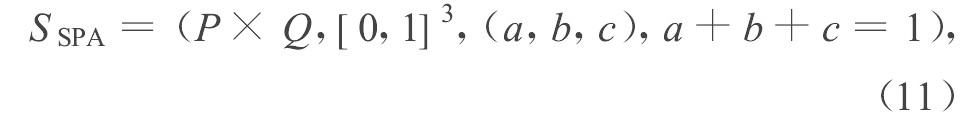
其中:P是论域U1上的幂集, Q是论域U2上的幂集, P × Q的任意一个元素构成了一个集对, 这个集对都被B =[0, 1]3 中的一个元素描述, F是一个三元组, 分别反映了集对的同异反, 约束是a+b+c=1。
SSPA中的任意一个元素可以表示为:r= ( (S1, S2) , (a, b, c) ) , 其中 (S1, S2) 是一个集对, (a, b, c) 是这个集对的同一度、差异度、对立度。S1和S2都是经典集合, 用统一集表示为
《图5》
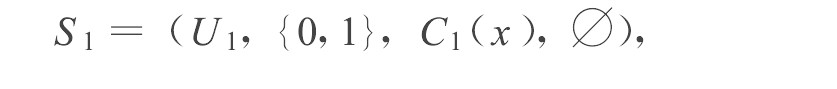
《图6》
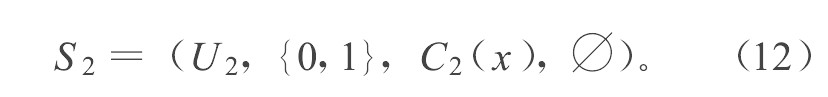
集对的统一集表示法反映了这样的思想:任意给定讨论范围内的一个集对, 都用一组a, b, c的值与其对应, 分别反映集对中两个集合的统一、差异和对立的程度。
2) 粗糙集合类[12]。
其中P是论域U的幂集, P × P的元素是一对U上的子集合, 分别表示P中元素的上下近似集。
值得一提的是, 上面表达的仅仅是粗糙集合类, 而传统意义上的粗糙集
其中X, R- (X) 和R- (X) 都是经典集合, 分别表示为统一集形式:
3) 模糊粗集[10,11]和广义粗集[12]。
如果式 (15) 中的X, R- (X) 和R- (X) 都是模糊集合, 那么, r就是一个粗糙模糊集。其中, X, R- (X) 和R- (X) 表示为统一集的形式:
式 (13) 相应地变成粗糙集合类, 可以表示为
F为论域U上的所有的模糊集合, 映射F1和F2也要变换成相应的模糊粗集定义的形式。并且约束中R也成为模糊的划分关系。
在式 (13) 的定义中, 如果对约束关系R不进行限制, 并修改相应的映射形式F1, F2, 那么, Srough中的任何一个元素就是一个广义的粗集。
《2.4统一集上的运算》
2.4统一集上的运算
在一般的集合论中, 都有关于集合与集合之间的运算, 例如, 集合的交、并、补。无论什么样的运算, 都是把一个或若干个集合映射到另一个集合。因此, 把集合的运算看成是这个集合所在论域上的幂集代数运算。在此, 给出统一集的同类集合、幂集等相关概念的定义。
定义1 (同类集合) 给定2个统一集:S1= (A1, B1, F1, J1) , S2= (A2, B2, F2, J2) 。 如果A1=A2=A, 并且B1=B2=B, J1=J2=J, 那么称S1与S2是定义在A上的同类集合。
定义2 (幂集) 在A上与S = (A, B, F, J) 同类的所有集合的总和称为S的幂集, 记为P (S) 。
不难看出P (S) 是一个经典集合, 同样可以写作统一集的形式
定义3 设给定两个定义在A上的同类统一集S1 = (A, B, F1, J) , S2 = (A, B, F2, J) , 其幂集都是P (S) , 则P (S) 上的一个二元运算定义为P (S) 上的映射σ: P (S) ×P (S) →P (S) 。 该二元运算是两个统一集S1和S2的二元运算。仿照此定义, 不难给出统一集的一元运算、n元运算的定义。
普通集合的交、并、补等运算可以描述成统一集的运算形式
r1为S1中的元素, r2为S2中的元素。如果要求x1=x2=x, 则σ作用在这2个元素上产生的像:
由此可见, 映射σ 实际上仅仅作用在A中的元素描述上, 也就是:
这样, 可以通过研究B中运算的性质来研究集合的运算。
如上所述, 统一集的运算可以看成统一集幂集上的代数运算, 而n阶统一集的幂集是n+1阶的统一集, 也就是说n阶统一集的运算可以看成n+1集合上的代数运算。因此, 对于一般的统一集, 可定义该集合上的代数运算。
定义4 (统一集的直积) 设两个统一集:S1和S2, r1和r2分别是S1和S2中的任意两个元素, 则S1×S2 = {< r1, r2>| r1是S1中的元素, r2是S2中的元素}, 称为S1与S2的直积, 其中 <, > 表示一个有序对。S1×S2是一个经典集合。
定义5 (统一集上的二元运算) 设S = (A, B, F, J ) 为一个统一集, 其上的任意两个元素为r1= (x1, F (x1) ) 和r2= (x2, F (x2) ) , S上的二元运算定义为σ: S×S→S, 也可写成
式中xωσ∈A, F (xσ) ∈B。 由此可见, σ 是由两部分构成的, 即
如果S是一个一阶以上的统一集, 那么, σA就是统一集运算。一元运算、n元运算都可仿照上面的方法给出定义。
《2.5关于界壳J的讨论》
2.5关于界壳J的讨论
前面提到, J是一个界壳
设S0为 n 维欧几里得空间Rn中的一个超球面, 其半径为1, 在S0上存在有限个界门Gm, m<∞, 则称S0构成了一个标准界壳
称由任一界壳B到J的一个映射W为壳函数。界壳有一个很重要的称为界壳套
把经典集合U以及定义在U上的一个二元运算σ组成的代数系统, 看成一个统一集, 这个统一集可以写成
如果对S中的J给予不同的限制, 那么就会构成不同的代数系统。设有第i种限制为Ji, 那么, 相应的代数系统为Si。如果Ji如下面的形式:
J1: ∅, 则S1为群胚。
J2: ∀a, b, c∈U, 有 (aσb) σc=aσ (bσc) 即结合律, 则S2为半群。
J3: 满足J2的约束, 并且, ∃e, ∀a∈U, 有aσe=eσa, 那么S3就是幺半群。
J4: 满足J2, J3的约束, 且∀a∈U, ∃a-1∈U, 有aσa-1=a-1σa=e, 那么S4就是群。
J5: 满足J2, J3, J4中的约束, 且∀a, b∈U, 有aσb=bσa, 则S5为交换群。
显然, J1⊂ J2⊂ J3 ⊂ J4 ⊂ J5形成一个界壳套, 而构成的代数系统也有这样的包含关系, S5 ⊂S4 ⊂ S3 ⊂ S2 ⊂ S1 。 因此, 不同的界壳也可以导出不同的集合或运算系统。它在统一集的构成中起了关键的作用。
《3 统一集在人工智能中的应用》
3 统一集在人工智能中的应用
统一集可以对人类的各种思维进行统一的表示, 把它应用到人工智能中将会有广阔的前景
《3.1统一集与模式识别》
3.1统一集与模式识别
模式是指存在于时间或空间中的事物所反映出来的信息, 如果可以区别它们是否相同或是否相似, 都可以称为模式
《3.1.1 直接识别[15]》
3.1.1 直接识别[15]
设给出的一个模式是A中的元素x, 那么, 对x的识别反应在这个x应该归为n类中的哪一个。首先, 计算x在这n类中的广义隶属度, 它们可以构成一个向量V= (F1 (x) , F2 (x) , …, Fn (x) ) , 反映x对于n种模式的隶属情况, 而所关心的是要把它归为哪一个类。如果说x归于第i类, 那么, 可用一个布尔向量表示为U= (0, 0, …, 0, 1, 0, …, 0) , 其中1是向量中的第i个元素。因此, 下面要寻找的是一个映射k, 它把V变成U, 映射k要视具体情况而定。例如, 在模糊模式识别时, k反映的是最大隶属原则, 而在很多情况下, k也可以是一个训练好的神经网络。
《3.1.2 间接识别[15]》
3.1.2 间接识别[15]
如果给定的待识别事物也用统一集Sx表示时 (Sx也是与Si同类的统一集) , 这比上面叙述的方法复杂了, 因此称其为间接识别。设Sx= (A, B, Fx, J ) , 并设A中有m个元素, 那么, A中的任意一个元素xj就会在Sx中有一个对应的广义隶属度Fx (xj) , 这个元素在第i个已知模式的统一集中也有一个对应的广义隶属度Fi (xj) , 这两个广义隶属度构成了一个对子 (Fx (xj) , Fi (xj) ) 。 这样对A中的任意一个元素和所有的n个统一集, 可构成一个矩阵[R]ij, [R]ij中的每一个元素都是一个广义隶属度所组成的对子。所关心的结果依然是待识别的对象归于哪一类, 也就是找到布尔向量U, 这也可通过映射k来完成, k可写成k ([R]ij) =U。 模糊间接模式识别的方法是把k分成两步来完成, 先把所有R中列向量映射成一个实数, 从而构成一个行模糊向量, 再把这个行模糊向量映射成布尔向量。
《3.2统一集与聚类分析》
3.2统一集与聚类分析
给出统一集的聚类分析方法
定义6 (统一关系) 设有两个经典集合A1、A2, 如果一个统一集S= (A, B, F, J ) 中的A=A1×A2, 那么称S为A1与A2上的统一关系。其中S中的任意一个元素写成
对经典集合A中的元素进行聚类分析是指找出一个对经典集合A的划分, 这样可把A中的元素分成若干个组, 每一组就是一个类。从经典集合论中知道, 一个A上的划分和定义在A上的等价关系是一一对应的。而一个A上的等价关系可以用一个布尔划分矩阵R来表示。为了描述一个集合A上的任意两个元素之间的关系, 可以运用不同的思维方式, 而这些思维方式等同于一个A上的统一关系。也可为每一个统一关系定义一个统一关系矩阵, 矩阵中的每一个元素都是一个广义隶属度。因此, 为了最终的聚类, 找到最终的映射k, 把统一关系矩阵映射成A上的布尔划分矩阵。同样, 映射k的确定可采用经典的一些运算方法, 也可用神经元网络、遗传算法等方法来实现。
《3.3统一集与逻辑推理》
3.3统一集与逻辑推理
众所周知, 集合论与逻辑是分不开的。经典集合论导致了数理逻辑的产生, 模糊集合论导致了模糊逻辑的产生……。因此, 不难得出结论, 一种特定的集合论对应一种特定的逻辑。逻辑是由命题和推理构成的, 如果把命题类比为集合, 把推理类比为集合之间的运算, 就可把逻辑与集合论等价起来了。例如, 经典集合以及由经典集合定义的交、并、补的运算系统与数理逻辑推理系统等价。集合对应着命题, 而集合之间的交、并、补运算对应着命题之间的合取、析取、否定的运算, 命题的真值可以被看成元素与集合之间的隶属。因此, 在数理逻辑中, 命题只有真、假两种值, 这是因为经典集合中的元素只有属于和不属于两种概念。而模糊逻辑是一种无穷真值的逻辑, 因为, 每个模糊命题的真值都是一个[0, 1]区间中的数, 这也正是模糊集合所反映的隶属度范围。
在此不难得出结论, 人脑的一类思维方法可以被看成一种形式的统一集, 而一种统一集所反映出来的隶属关系和集合之间的运算则对应了一种形式的逻辑体系。给定一个统一集S, 并且在S上定义了若干个统一集的运算, 则构成一个统一集的运算系统, 可表示为
《图7》
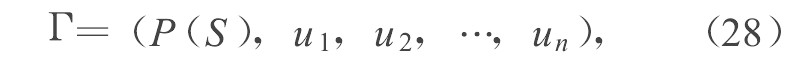
其中S是P (S) 表示S的幂集, u1, …, un是定义在P (S) 上的运算。这个运算系统等价于一个逻辑推理系统, 可写为
《图8》
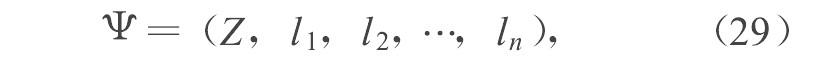
其中:Z为系统中所有的命题的集合, l1, …, ln是逻辑命题的连接运算, 与上面u1, …, un是一一对应的。这样, 所有逻辑推理都可以等价成集合与集合之间的运算。
值得讨论的是对于一类特殊的非普通统一集S= (A, B, F, J ) , 其中B=An, 表示B是A的n重直积。因此, F可分成n个分量 (F1, F2, …, Fn) , 其中每一个分量都是一个作用在A上的变换。而A中的任意一个元素X本身就是一个统一集。因此, 根据上面的论述, 这些X以及不同X之间的运算, 可构成集合运算系统Γ, 并且等价于一种逻辑推理系统Ψ。自然地可以把Fi作为一种变换加到Γ中, 对应的也就是在逻辑系统Ψ中定义了一种新型的运算。
为此, 可以将粗糙集合与模态逻辑的等价作为具体例子进行说明
其中:P是论域U上的幂集, P×P中的元素是一对U上的子集合, 分别表示集合的上下近似集, J为U上的等价关系R。这里B =A2, 也就是n =2, 可以看到F1和F2都是P上的一个变换。P中的任何一个元素都是一个经典集合, 可以给这些集合定义运算, 设为普通的交、并、补。那么, F1、F2可以看成是P中的变换, 把它加入普通集合的运算系统中。这样, 定义了一个集合运算系统:Γ= (P, ∩, ∪, ~, F1, F2) , 这个集合运算系统等价于模态逻辑系统S5 :Ψ= (∅, ∧, ∨, ┐, ◇, □) , 见表1。
若按照统一集的形式定义一种新的集合, 就相应地定义了一种新形式的逻辑。反之, 给出一种形式的逻辑系统, 可以找到与它对应的统一集形式运算系统。值得讨论的是统一集中的约束界壳J, 当把统一集运算系统等价为逻辑推理系统时, 统一集的约束J等价于逻辑推理中的约束作用。因此, 约束的逻辑也可在统一集中找到对应的概念。
《3.4统一集与机器学习》
3.4统一集与机器学习
机器学习
用统一集可以表示人类不同的思维方法, 对一个问题的描述就可用统一集的模型。一个统一集模型S= (A, B, F, J) 有四个元素, 一般认为描述问题范围或论域的A是已知的, 剩下的3个元素B, F, J都是不容易建立的。这里, 可通过外部输入的专家经验, 也可利用机器学习的方法, 来确定各种要素B, F, J。在一些传统的机器学习中, 要学习的参数可能很少。比如用神经网络的方法学习模糊集合中的隶属度, 要搜索的空间就是[0, 1]区间。而这里由于统一集有更加广阔的形式, 所以, 待搜索的空间会更加广阔, 对于问题的描述有了更加广泛灵活的形式。如对一个概念进行学习, 传统的机器学习方法仅仅提供建立模糊集合的形式, 而用统一集时, 根据问题的具体情况, 机器会自动学习采用什么样的问题描述域B, 以及采用什么样的映射形式F等等。由此, 通过学习建立的模型将会有更好的应用效果以及推广范围。
另外, 统一集理论还为创建新的学习算法提供了很好的途径。传统的粗糙集合的机器学习方法是利用对一个二维的条件决策表 (CD表) 进行化简, 从而得到简单的规则而达到从给定的数据中得出知识的目的。文献
《3.5统一集与智能决策》
3.5统一集与智能决策
随着科技的进步, 人们面临的将是越来越复杂的宏观复杂大系统
另外, 在考虑复杂的智能系统时, 约束J是需要考虑的一个重要的因素。根据界壳论
综合上面的讨论, 统一集论应用到宏观复杂大系统时可以总结为图1所示。由图1不难看出, 这套基于统一集的分析方法, 适用于宏观系统的决策问题, 也是利用统一集解决一般问题的方法。
《图10》
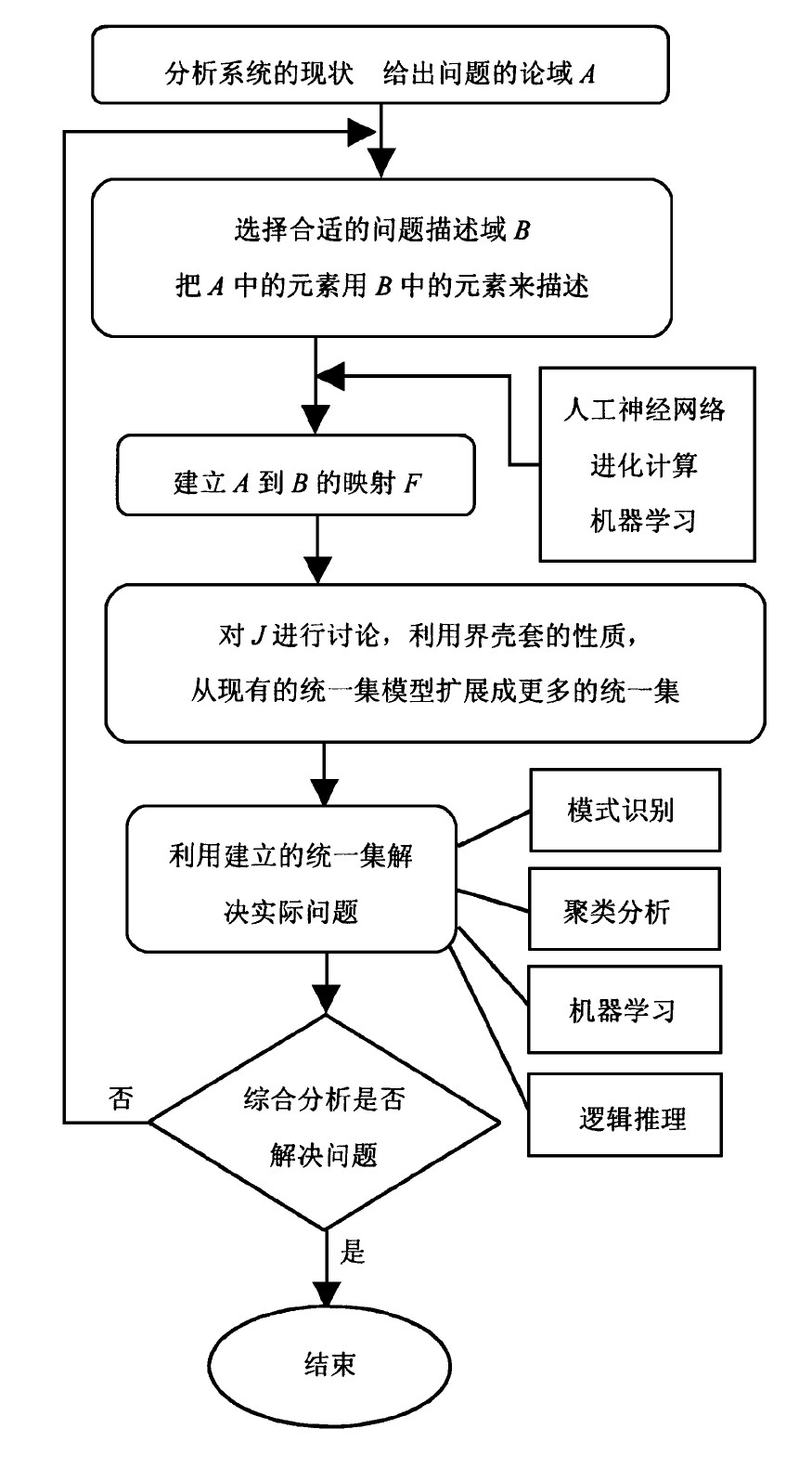
图1 统一集在宏观复杂系统中的应用Fig.1 Application of all set in macro complex system
《4 结语》
4 结语
通过本文的论述, 可以清楚地看出, 统一集给出了当前多种集合论的统一描述形式, 对集合论所共有的一些运算性质进行了讨论, 并结合在人工智能的几个方面的应用进行了初步探讨。然而一个理论仅仅能够包容现有的理论是不够的。有了统一集论的形式, 不仅可对当前的各种集合论进行解释, 而且还可按照统一集论的方法给出新的集合类型的定义。如果把现有的多种集合论相互结合, 也可提出更多的集合论形式。由于一种统一集对应人类的一种思维模式, 所以为了使人工智能技术能够模拟人的思维, 统一集是一个必不可少的工具。














 京公网安备 11010502051620号
京公网安备 11010502051620号




