《1 引言》

1 引言

当今,世界截流技术的发展趋势是以立堵法逐渐代替平堵法。事实上,20世纪60年代以来,国内外绝大多数工程均采用立堵截流,平堵法已很少采用。形成这种发展趋势的主要原因是立堵截流中所存在的问题逐渐得到了解决,而平堵截流的固有缺点仍然存在。然而,三峡工程大江截流又暴露出一个立堵截流中的新的重大问题,即戗堤边坡的大规模坍塌。实践表明,在截流龙口水深较大的情况下,戗堤边坡的坍塌严重影响截流施工的顺利进行,直接威协堤头施工人员及施工机械的安全,所以,加强对这个问题的研究就显得非常重要,而探明戗堤边坡坍塌的原因是其中的首要问题。

《2 戗堤边坡坍塌的影响因素》

2 戗堤边坡坍塌的影响因素

在以往很多工程的截流模型试验中,戗堤边坡上局部块石群或其底部覆盖层不稳定的现象时有发生。例如,在澜汾江大朝山水电站的截流模型试验中,在隧洞不参加分流的情况下,用粒径相当于20cm以下的石渣料进行预进占,当抛投进占至龙口戗堤顶口门宽度72.4m(水面宽度69.5m)时,抛投料开始流失,并引起坡面上大片石渣向下潺移,此时龙口最大水深约为16m,戗堤轴线断面最大流速为3.17m/s。从总的来看,这种坍墩是在流速较大、水深较小的情况下发生的,其塌方频率何、面积小。

与以上现象明显不同的是,在长江三峡工程大江截流工程中,戗堤端部的坍塌现象要严重得多。这一点在其模型试验及原型观测资料上可以看得比较清楚,其特点是流速较小、水深较大,坍塌频率、塌方面积较大,对工程的危害严重^[1]。

从定性上分析,导致两类坍塌现象的主要因素有:

1) 抛投材料的抗冲能力。当龙口水流流速大于抛投材料的抗冲能力时,边坡上的材料开始部分流失,已稳定的边坡受到龙口水流和戗堤透透水流的共同作用,从而引起边坡冲刷,导致其上部塌方。这种坍塌一般为面积较小、危害不大的局部塌方。

2) 戗堤基础的抗冲能力。当河床覆盐层可冲性较强、无护底或护底措施不当、龙口水流流速较大时,坡脚容易被水流淘空,造成戗堤边坡的塌方。在水深不大时,这种坍塌一舱也为局部塌方。

3) 龙口水深。由于龙口水深较大,抛投料人水后不能一次到达戗堤底部,戗堤前沿呈上部降、下部缓的折线型边坡。材料在戗堤上部逐深积累,形成暂时稳定的堆积体,在外部荷载(如水流扰动、重型施工机械压力等)的作用下,堆积体内部应力发生变化,超过临界状态时,便会发生坍塌。这种现象已经为模型实验所证实。

4) 抛投材料的力学性质。水流的冲(淘)剧、抛投材料的浸水湿化以及外部荷载作用等因素都会使堆石内部应力发生变化,当剪应力超过抗剪强度时,就会引起坍塌。

5) 抛投材料的浸水湿化。在连续高强度抛投过程中,材料入水后没有充分湿化便被下一层材料覆盖,之后由于渗透水流的作用,堆积体内部被水浸泡、湿化,摩擦力逐渐降低,外部扰动(如水流脉动)的作用便会诱发坍塌。

在流速较小的深水截流中,戗堤坍塌与否、坍塌规模大小,主要由下面三个因素决定。为了阐明其机理,现针对堆石内部的应力变化和抛投材料的浸水湿化做进一步的理论分析。

《3 戗堤堆石微结构模型应力分叉特性》

3 戗堤堆石微结构模型应力分叉特性

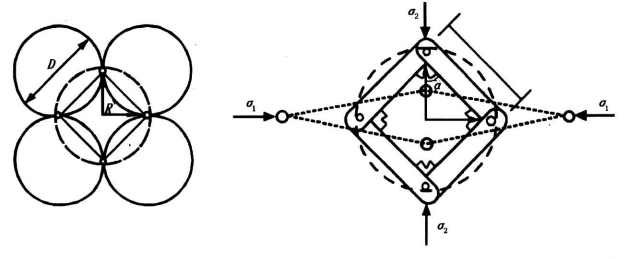
下面引入一个微结构模型口,如图1所示。模型假定各种形状的抛投体均可以化为体积相同的球体,而且饲堤堆石的三维孔隙结构可以简化为平面问题。模型具有以下特征:a,圆形颗粒化为轻质刚性杆,菱形孔隙采用铰接的四连杆系统模拟;b.颗粒之间的接触摩阻力用杆系的联系拉伸弹簧来模拟,其弹性系数为K;c.杆长为,模拟结构元的初始状态由a角确定,a=π/4。

《图1》

图1 戗堤堆石不稳定孔隙微结构模型

Fig.1 Micro model of unstable small opening of the dike rockfil

《3.1 微结构模型的应力分岔特性》

3.1 微结构模型的应力分岔特性

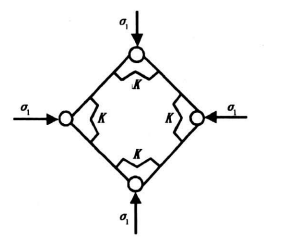
考虑以σ₁为参数,K为常量,如图2所示。

《图2 》

图2 微结构元的理想应力状态

Fig.2 The ideal stress state of the micro unit

设结构微元产生一个x角的微小变化,则两对弹簧将分别产生2x的伸长或压缩变形,系统的总势能函数为弹簧弹性势能与杆件系统变形势能之和:

\(V\left(x, \sigma_{1}\right)=8 K x^{2}+4 R \sigma_{1}(\cos x-1)\)（1）

下面推求系统的奇异点。系统的静平衡状态由以下方程决定:

\(\bar{g}\left(x, \sigma_{1}\right)=\partial V / \partial x=16 K x-4 R \sigma_{1} \sin x=0\)（2）

由于\(\bar{g}(0,4 K / R)=0\)，\(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\bar{g}_{x}(0,4 K / R)=0 \),所以,点\( \left(x, \sigma_{1}\right)=(0,4 K / R) \)是\( \bar{g}\left(x, \sigma_{1}\right)\)的一个奇异点。作以下平移变换,令\(\sigma_{1}=\mu+4 K / R\),则(2)式化为:

\(g(x, \mu)=16 K x-(4 R \mu+16 K) \sin x=0\)（3）

显然,g(0,0)=g_x(0,0)=0,因此,点(x, μ)=(0,0)是g(x, μ)的一个奇异点。而且可以计算:g(0,0)=g_x(0,0)=g_xx(0,0)=g_μ(0,0)=0

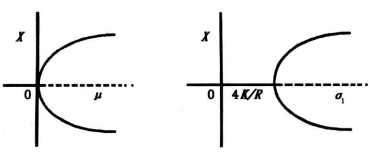
g_xxx(0,0)=16K＞0,g_xμ(0,0)=-4R＜0,所以,g(x, μ)=0与GS范式h(x, μ)=x³-μx 强等价^[3]。从而,在(0,0)处,方程g(x, μ)=0与方程h(x, μ)=0有相同的分叉性态,点(0,0)是叉形点,g(x, μ)=0在点该处出现超临界叉形分叉,见图3。

《图3》

图3 分叉图

Fig.3 Bifurcation diagram

《3.2 g(x, μ)的扰动系统》

3.2 g(x, μ)的扰动系统

方程(1)及(2)是对戗堤堆石内部应力作了简化后得到的理想模型,而真实状态是,作用在结构微元上的应力并不相等。为了消除这种差异,可以把真实状态看成是理想状态的一个扰动,进而去分析这种扰动对方程的分叉性态的影响。

3.2.1 理想系统的普造开折_由于g(x, μ)=0与h(x, μ)=0强等价,因此它们的余维数相同,即:两者普适开折的参数个数都为2。从理想系统的物理意义上来看,扰动主要来自以下两个方面:

1) 考虑到作用在结构微元垂直与水平方向的应力不相等,因此在水平方向上引人小参数σ₂;

2) 当所有外力为零时,假定结构微元已有一个微小的角度变化x₀,即初始平衡位置为:a≠π/4。

图4为引进附加的小参数σ₂和x₀之后的扰动系统,其总势能方程为:

\(\begin{array}{c}V^{*}\left(x, \sigma_{1}, \sigma_{2}, x_{0}\right)=8 K\left(x-x_{0}\right)^{2}+4 R \\{\left[\frac{1}{2}\left(2 \sigma_{1}+\sigma_{2}\right) \cos x-\frac{1}{2} \sigma_{2} \sin x-\frac{1}{2}\left(2 \sigma_{1}+\sigma_{2}\right)\right]}\end{array}\)，（4）

静平衡状态由下述方程决定:

\(\begin{array}{c}G^{*}\left(x, \sigma_{1}, \sigma_{2}, x_{0}\right)=\frac{\partial V^{*}}{\partial x}=16 K\left(x-x_{0}\right)- \\4 R\left[\frac{1}{2}\left(2 \sigma_{1}+\sigma_{2}\right) \sin x+\frac{1}{2} \sigma_{2} \cos x\right]=0\end{array}\)，（5）

令\(\sigma_{1}=\mu+4 K / R\),代入上式可得;

\(G\left(x, \mu, \sigma_{2}, x_{0}\right)=16 K\left(x-x_{0}\right)-4 R \cdot\left[\frac{1}{2}\left(2 \mu+\frac{8 K}{R}+\sigma_{2}\right) \sin x+\frac{1}{2} \sigma_{2} \cos x\right]=0\) ，（6）

《图4》

图4 g(x, μ)的扰动系统

Fig.4 The turbulence system of g(x, μ)

因为G(x, μ, 0, 0)=g(x, μ),所以G(x, μ, σ_2, x₀)是g(x, μ)的一个2一参数开折。

下面确定G(x, μ, σ_2, x₀)是g(x, μ)的普适开折。因为g(x, μ)与h(x, μ)=x³-μx强等价,所以判别G(x, μ, σ_2, x₀)是g(x, μ)的普适开折的充要条件是:

\(\operatorname{det} A(0,0,0,0) \neq 1\)  （7）

\(A=\left(\begin{array}{cccc}0 & 0 & g_{x \mu} & g_{x x x} \\0 & g_{x \mu} & g_{\mu \mu} & g_{\mu x x} \\G_{\sigma_{2}} & G_{\sigma_{2} x} & G_{\sigma_{2} \mu} & G_{\sigma_{2} x x} \\G_{x_{0}} & G_{x_{0} x} & G_{x, \mu} & G_{x_{0} x x}\end{array}\right)\)   (8)

可以计算

\(\operatorname{det} A=\left|\begin{array}{cccc}0 & 0 & -4 R & 16 K \\0 & -4 R & 0 & 0 \\-2 R & -2 R & 0 & 2 R \\-16 K & 0 & 0 & 0\end{array}\right|=-512 K R^{3}\)      

由于K,R≠0,所以det(A)≠0,因此G(x, μ, σ_2, x₀)是g(x, μ)的一个普适开折,它包含了g(x, μ)的所有扰动函数。也就是说,理想系统g(x, μ)=0在受到σ_2, x₀扰动后还会出现更加复杂的分叉性态。

3.2.2  G(x, μ, σ_2, x₀)的保持性    分析G的保持性问题,就是讨论开折参数(σ_2, x₀)对普适开折G的分叉的影响,由于G包含了g的所有扰动,因此G的静态分叉特性也就反映了g受扰后可能出现的各种分叉性态。对此,我们将G相应的偏导数代人符合\(\mathscr{B}\)(分支点集)、\(\mathscr{H}\)(滞后点集)、\(\mathscr{D}\)(双极限点集)的方程组,通过计算可得,

\(\mathscr{B}=\left\{\left(\sigma_{2}, x_{0}\right) \in R^{2} \mid \sigma_{2}=-\frac{8 K}{R} x_{0}\right\}\)   (9)

\(\mathscr{H}=\left\{\left(\sigma_{2}, x_{0}\right) \in R^{2} \mid \sigma_{2}=\frac{8 K\left(1-\cos x_{0}\right)}{R\left(\cos x_{0}-\sin x_{0}\right)}\right\}\)   (10)

\(\mathscr{D}=\phi \)

因此G的转迁集\(\Sigma=\mathscr{B} \cup \mathscr{H}\)由(9)及(10)式可知\(\mathscr{B}\)\(\mathscr{H}\)把参数\(\left(\sigma_{2}, x_{0}\right) \)平面分成了四个子区域,在子区域Ⅰ、Ⅱ、Ⅲ、Ⅳ中,G的分叉图是持久的,分叉图上的奇异点都是极限点;在集\(\mathscr{B}\)(即直线\(\sigma_{2}=-\frac{8 K}{R} x_{0}\)上,G的分叉图上有分支点,在集\(\mathscr{H}\)(即曲线\(\sigma_{2}=\frac{8 K\left(1-\cos x_{0}\right)}{R\left(\cos x_{0}-\sin x_{0}\right)}\))上,G的分叉图上有滞后点,在原点处,G的分叉图上有叉形点(它既是分支点,也是滞后点),这些分叉图都是非持久的(退化的)。

《4 戗堤堆石结构的湿化机理分析》

4 戗堤堆石结构的湿化机理分析

考虑以K为参数,以σ₁为常量,如图2所示,则系统的总势能方程为:

\(V(x, K)=8 K x^{2}+4 R \sigma_{1}(\cos x-1)\)。(12)4.1奇异点附近的分叉特性

系统的静平衡状态取决于下面的方程:

\(\bar{s}(x, K)=16 K x-4 R \sigma_{1} \sin x=0\),(13)令\(\mu=K-R \sigma_{1} / 4\),则式(13)变为:\(s(x, \mu)=\left(16 \mu+4 R \sigma_{1}\right) x-4 R \sigma_{1} \sin x=0\),(14)显然,s(0,0)=s_x(0,0),因此,点(0,0)是s(x,μ)的一个奇异点。同样可以计算:\(\begin{array}{l}s(0,0)=s_{x}(0,0)=s_{x x}(0,0)=s_{\mu}(0,0)=0 \\s_{x x x}(0,0)=16 K \succ 0, s_{x \mu}(0,0)=16 \succ 0\end{array}\)

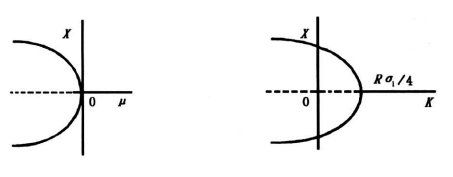
于是,\(s(x, \mu)\)与\(h(x, \mu)=x^{3}+\mu x\)强等价,从而在点(0,0)处\(s(x, \mu) =0\)与\(h(x, \mu) =0\)有相同的分叉性态。点(0,0)仍然是叉形点,而\(s(x, \mu)\)在该处出现亚临界叉形分叉,其分叉如图5所示。

由此可见,当K因浸水湿化而降低至R_σ1/4时,系统\(\bar{s}(x, K)=0\)解的数目将出现突然变化,对照图3,我们发现两者分叉图的形状相同。不同之处在于:前者是由于在荷载作用而使应力增

《图5》

图5 分叉图

Fig.5 Bifurcation diagram

大到σ1=4K/R时引起的分叉。而后者是由于水的湿化作用而使K降低到K=R_σ1/4引起的分叉。这两种分叉的实际物理意义是:截流戗堤堆石孔隙微结构将发生失稳,即产生坍塌现象。

《4.2 扰动系统》

4.2 \(s(x, \mu)\)的扰动系统

下面考虑\(\bar{s}(x, K)=0\)的一个扰动系统,如图6所示,扰动来自以下两个方面:

1) 与前面的情况相类似,在水平方向上引人附加小参数σ2;

《图6》

图6 \(s(x, \mu)\)的扰动系统

Fig.6 The turbulence system of \(s(x, \mu)\)

2) 由于K模拟的是单位长度上的颗粒之间的摩阻力,因此参数K除了因水的湿化作用而降低以外,根据库仑定律,它还可能随应力的变化而变化。为此引入小参数,并假定它具有以下性质: a. 它反映了由σ2引起的K值变化,与因水的湿化作用而引起的变化值无关,并且这两种变化可以叠加; b. 它是一个无因次的量,且0<|m|<1。

扰动系统总势能方程为:

\(\begin{array}{l}V^{*}\left(x, K, \sigma_{2}, m\right)=8 K(1+m) x^{2}+4 R \cdot \\{\left[\frac{1}{2}\left(2 \sigma_{1}+\sigma_{2}\right) \cos x-\frac{1}{2} \sigma_{2} \sin x-\frac{1}{2}\left(2 \sigma_{1}+\sigma_{2}\right)\right]}\end{array}\),  (15)

静平衡状态方程为:

\(\begin{array}{l}S^{*}\left(x, K, \sigma_{2}, m\right)=16 k(1+m) x- \\4 R\left[\frac{1}{2}\left(2 \sigma_{1}+\sigma_{2}\right) \sin x+\frac{1}{2} \sigma_{2} \cos x\right]\end{array}\)    , (16)

令\(K=\mu+R \sigma_{1} / 4\)则得：

\(\begin{array}{c}S\left(x, \mu, \sigma_{2}, m\right)=\left(16 \mu+4 R \sigma_{1}\right)(1+m) x- \\4 R\left[\frac{1}{2}\left(2 \sigma_{1}+\sigma_{2}\right) \sin x+\frac{1}{2} \sigma_{2} \cos x\right] \end{array}\)  。（17）

因为\(S\left(x, \mu, \sigma_{2}, m\right)=s(x, \mu)\),所以\(S\left(x, \mu, \sigma_{2}, m\right)\)是\(s(x, \mu)\)的一个2-参数开折。由于\(s(x, \mu) \)与\(h(x, \mu)=x^{3}+\mu x\)强等价,所以\(S\left(x, \mu, \sigma_{2}, m\right)\)是\(s(x, \mu)\)

的普适开折的判断短阵形式为:

\(A=\left(\begin{array}{cccc}0 & 0 & s_{x \mu} & s_{x x x} \\0 & s_{x \mu} & s_{\mu \mu} & s_{\mu x x} \\S_{\sigma_{2}} & S_{\sigma_{2} x} & S_{\sigma_{2} \mu} & S_{\sigma_{2} x x} \\S_{m} & S_{m x} & S_{m \mu} & S_{m x x}\end{array}\right)\)

可以计算，

\(\operatorname{det} A=\left|\begin{array}{cccc}0 & 0 & 16 & 4 R \sigma_{1} \\0 & 16 & 0 & 0 \\-2 R & -2 R & 0 & 2 R \\0 & 4 R \sigma_{1} & 16 & 0\end{array}\right|=2048 R^{2} \sigma_{1}\)

由于\(R \neq 0, \sigma_{1} \neq 0\),所以\(det (A) \neq 0, S \left(x, \mu, \sigma_{2}, m\right)\)是\(s(x, \mu)\)的一个普适开折。

下面研究理想静平衡系统。\(s(x, \mu) =0\),在受到\(\sigma_{2}\),m的扰动后可能出现的分叉性态。通过计算可以得到\(\mathscr{B}\)、\(\mathscr{H}\)、\(\mathscr{D}\)集:

\(\mathscr{B}=\left\{\left(\sigma_{2}, m\right) \in R^{2} \mid \sigma_{2}=0, m=0\right\}\) ，   （18）

\(\mathscr{H}=\left\{\left(\sigma_{2}, m\right) \in R^{2} \mid \sigma_{2}=2 \sigma_{1} m\right\}\)，     （19）

\(\mathscr{D}=\phi\)   ,  (20)

\(S\left(x, \mu, \sigma_{2}, m\right)\)的转迁集\(\Sigma=\mathscr{B} \cup \mathscr{H}\),\(\mathscr{B}\), \(\mathscr{H}\)把参数\(\left(\sigma_{2}, m\right)\)平面分成了二个区域,在子区域I、II中S的分叉图是持久的,分叉图上的奇异点都是极限点,在集8(即原点)上,S的分又图是退化的,分叉图上的奇异点是叉形点;在集\(\mathscr{H}\)(即直线\(\sigma_{2}=2\sigma_{1}m\))上,S的分叉图也是退化的,分叉图上有滞后点。

《5 分析与结论》

5 分析与结论

1) 模型上戗堤边坡坍塌的根本原因。以前的研究认为^[4],戗堤高频率、大规模坍塌的主要原因是龙口的水深较大。减小水深当然可以有效地控制坍塌。但是,由于在模型上采用的是粒径较均匀的抛投材料,它们在戗堤的很大范围内形成了与本文所用的微结构模型基本相似的孔隙结构。因此,当堆石内部应力增加或材料的K值降低到一定程度时,微结构将出现分叉现象,引起结构突然失稳,戗堤仍然会发生坍塌。因此,从更一般的意义上讲,本文认为结构应力状态的变化和抛投材料的浸水湿化是戗堤边坡坍塌的根本原因。

2) 戗堤边坡坍塌的偏差分析。如果模型与原型完全相似,则其土塌情况也应该一致,但三峡工程大江截流的实践证明,模型试验戗堤边坡坍塌的可能性和范围比大江截流实施时要大,造成这种差别的主要原因有:其一,比尺效应问题。由于戗堤边坡是一个无量纲数,因此在将模型抛石粒径准确模拟原型时,模型边坡与原型边坡一般都不相似,模型边坡与原型边坡的内摩擦角也存在较大差别,这样,模型与原型的稳定边坡自然不相同^[5]。古外,在模型上还难以模拟原型上重型自卸汽车对戗堤的静力(或动力)施工荷载。这些差别造成了模型与原型坍塌情况的不一致;其二,模型与原型抛投材料的差别。截流模型试验上所采用的抛投材料粒径相对比较均匀,这种情况与本文的假设条件比较接近。因此,上文的有关结论运用于模型试验是合理的;而对于实际截流施工来说,群体抛投材料多采用具有一定级配的石渣混合料,材料在孔隙率和孔隙形态方面与前面的假设有较大差别。因此,有关结论对于原型来说只能是近似的、初步的。但就其本质来说,无论是模型还是原型,都存在着应力状态的变化和材料的浸水湿化对戗堤边坡稳定的影响问题,这是客观存在的规律,只不过模型戗堤堆石的内部结构在很大范围内接近本文所采用的理想模型,而原型与此接近的结构可能是小范围的、局部的,这从古一个角度说明了模型戗堤边坡突然坍塌的可能性以及坍塌范围比原型要大的原因。

3) 根据以上分析,为了防止或减少戗堤边坡的坍塌,在深水截流施工时,本文建议: a. 各理安排进占计划,根据各段水深情况确定合理的抛投强度,避免停工现象; b. 除了围堰结构上的要求以外,在其他部位应尽量避免使用粒径均匀、形状接近球形的抛投材料; c. 对于普道采用的石渣混合料,应减少其中的含泥量,以降低水对材料湿化的影响程度;d. 避免大吨位载重汽车过于接近堤头边缘和直接卸料人水,以减少对胎堤边坡的冲击和内部应力的扰动。在三峡工程大江截流实际施工中，采用平抛垫底的措施减少了龙口水深，从而使 坍塌得到了有效的控制，同时，在非龙口段和龙口 段的进占过程中，采取了诸如汽车卸料配合推土机 赶料、适时安排抛投强度等多项综合性的防塌措 施，收到了良好的效果，胜利完成了大江截流^[1]。 本文通过机理分析所提出的几点建议与三峡工程实 际截流的部分施工措施基本吻合，但是，用静态分 叉和奇异性理论对俄堤坍塌的原因进行分析，在理 论上是否成熟，还有待进一步验证。