《1 前言》

1 前言

离群数据（outlier）是在数据集中与众不同的数据，使人怀疑这些数据并非随机偏差，而是产生于完全不同的机制[1] 。目前已经出现了一些高效的离群点检测挖掘算法：基于聚类的、统计的、距离的、深度的以及基于密度的方法等 5 种类型[2 ~ 6] 。但大多数离群点检测算法对高维数据的异常检测效果都不是很理想。高维空间离群点检测与其他数据集的离群点检测差别甚大的原因主要有两个：a. 对高维数据的估计需要的样本个数与维数构成指数增长的关系，即机器学习中的“维数灾难”（ curse of dimensionality） [7] ；b. 大量的数据分析问题本质上是非线性的，甚至是高度的非线性。一种常用的做法是在保持数据所含感兴趣信息的前提下，尽可能降低数据的维数，即降维。 LLE 是 Roweis 和 Saul 于 2000 年提出的一种解决非线性问题及克服维数灾难问题的方法[8] ；由文献[9]和[10]中可知基于距离的离群点最早是由 Knorr 和 Ng 提出的，他们把数据看作高维空间中的点，离群点被定义为数据集中与大多数点之间的距离都大于某个阈值的点。基于距离的离群点定义包含并拓展了基于统计的思想，即使数据集不满足任何特定分布模型，它仍能有效地发现离群点。此算法的一个主要缺陷是要计算所有点之间的距离，每计算一个点的距离就要扫描一次数据集，对于大数据集，其 I/O 次数常常使得算法的计算效率非常低。由此，基于 LLE 算法和基于距离方法的融合，提出了一种思路———基于流形学习的离群点检测方法，其基本思想是：该算法利用 LLE 算法对高维非线性数据进行维数约减，对从高维采样数据中恢复得到低维数据集，通过邻域数的选取，结合降维后数据点之间距离调整，并根据文章提出的离群点权值判别式进行权值数据的判别，同时，在判别基础上，设定分段线性处理，再利用局部邻近点加权，最终确定离群点。实验表明此算法能够快速处理带有离群点的非线性高维数据集，结果与对象空间分布顺序无关，并且效率优于已有的同类基于距离的离群点检测算法。

《2 LLE 算法简介》

2 LLE 算法简介

LLE 算法是映射数据 X ＝｛ x1 ，x2 ，…，xn ｝，xi ∈ RD 到数据集 Y ＝｛ y1 ，y2 ，…，yn ｝，yi ∈ Rd （D ＞ d）。该算法主要包括３步：

第一步，对高维空间中的每个样本点 xi （ i ＝ 1 ，2 ，…，n），计算它和其他 n －１个样本点之间的距离，根据距离的大小，选择前 K 个与 xi （ i ＝ 1 ，2 ，…， n）最近的点作为其邻近点，采用欧氏距离来度量两个点之间的距离，即 dij ＝ | xi － xj | ；

第二步，对每个 xi （ i ＝ 1 ，2 ，…，n），找到它的 K 个近邻点之后，计算该点和它的每个近邻点之间的权值 ，即最小化：

其中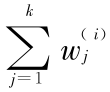，＝１，如果 xj （ j ＝ 1 ，2 ，…，n）不是 xi（ i ＝ 1 ，2 ，…，n）的近邻，则 ＝０；

第三步，根据高维空间中的样本点 xi （i ＝ 1 ，2 ，…，n）和它的近邻 xj （j ＝ 1 ，2 ，…，K）之间的权值 来计算低维嵌入空间中的值 yi 和 yj 。由于在低维空间中尽量保持高维空间中的局部线性结构，而权值 代表着局部信息，所以固定权值 ，使下面的损失函数最小化：

其中， M ＝（ I - W）T （ I - W）。

要求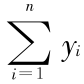 = 0 且 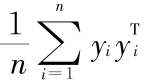 = 1 , ，以使 min ∈（Y）对平移、旋转和伸缩变化都具有不变性，使 min ∈（Y）最小化的解为矩阵 M 的最小几个特征值所对应的特征向量构成的矩阵 Y 。取M 最小的 m + 1个特征值对应的特征向量，去掉其中最小的特征值对应的特征向量，剩余的 m 个特征向量组成的矩阵就是低维空间中所得特征向量。

《3 基于流形学习的离群点检测方法》

3 基于流形学习的离群点检测方法

《3.1 邻域数的选取和改进距离定义》

3.1 邻域数的选取和改进距离定义

最近邻域最佳选取的原因在于大量的最近邻域可以促成流形小规模结构的消除及整个流形的平滑。相反，太少邻域可能误将连续的流形划分成脱节的子流形。可参照文献 [11] 原则按下式进行选取：

Dx 是输入空间 X 的欧氏距离矩阵，Dy 是得到嵌入的低维流形 Y 的欧氏距离矩阵，ρ 是他们之间的相关系数。

同时，对于降维后数据集分布中含有离群点的样本集，近邻点个数 k 的选取对实验结果影响较大。在样本点分布稀疏的区域，k 个近邻点所组成的局部邻域显然要比在样本点分布比较密集的区域大，可以通过以下对数据点之间距离的调整来降低它受样本点分布的影响。

对于 LLE 算法降维后分布中含有离群点的样本集，由于 LLE 算法能够实现高维输入数据点映射到低维坐标系，同时保留邻接点之间的关系，即固有的几何结构得到保留。因此，对降维后所得数据集，可以调整数据点之间的距离，以有利于离群点的发现。

我们知道在样本点分布稀疏的区域，近邻点所组成的局部邻域应该要比在样本点分布比较稠密的区域大，所以需要对原有的欧氏距离公式改进，改进距离如下：

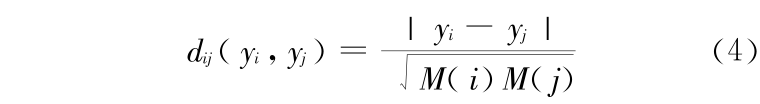
其中， M（i），M（j）分别表示 yi （ i ＝ 1 ，2 ，…，n）， yj （ j ＝ 1 ，2 ，…，n）和其他点之间的平均值，采用改进的距离寻找离群点。

的分子是普通的欧氏距离，分母是数值，所以容易证明给出的新距离满足距离定义的要求，即

1）   0 ，当且仅当 yi ＝ yj 时成立，满足距离的非负性；

2）满足距离对称性要求：

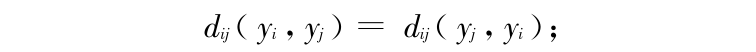
3）满足三角不等式要求，即

新的距离使处于样本点分布较密集区域的样本点之间的距离增大，而使处于样本点分布较稀疏的区域的样本点之间的距离缩小，这样会使降维后的样本数据集整体分布趋于均匀化，有利于近邻点计算，从而使数据集中的离群点更加突出。同时距离公式可设定所需的距离尺度用于下面的判别定理。

《3.2 离群点的权值判别定理》

3.2 离群点的权值判别定理

经过 LLE 算法降维，包括离群点的低维数据集是通过权值 W 计算而得，离群点权值的变化情况可由以下定理判别。

令 y0 代表 yi ，yi 所代表相应的真实值，U（y0）代表 y0 的邻域，设 y1 ，y2 ，…，yk ∈ U（y0），则

令 y′i ＝ yi ＋ di （i ＝ 0 ，1 ，2 ，…，k）代表相应的离群点，以及相应的

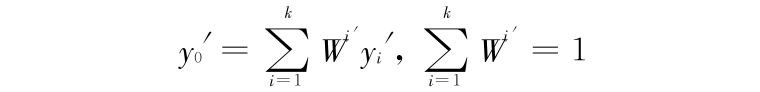
若再令

以及

于是有

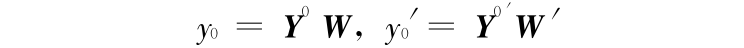
其中， 代表 y0 点的邻域矩阵。

定理在上述记号下，各离群点之间，不同真实值之间，以及 W′ 与离群点之间是相互独立的，各离群点是同均值（0），同方差的，并且记δW ＝ W′－ W ，有如下判别式：

其中，‖·‖取为欧几里德范数， 为 的最小非零特征值，di 代表 d 的第 i 个分量：

证明：由 y′i ＝ yi ＋ di（i ＝ 0 ，1 ，…，k）可见

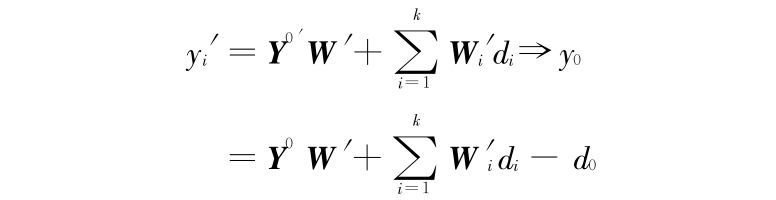
进一步有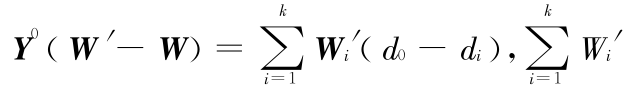

即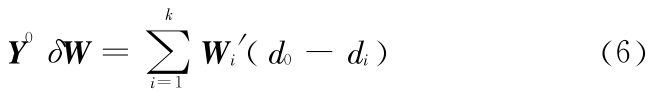 

由于离群点是独立的，则有

记 的正交分解为 = 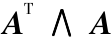，其中

A 为正交矩阵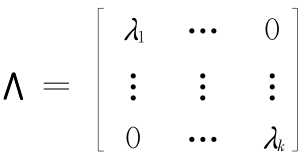，。由于，，所以

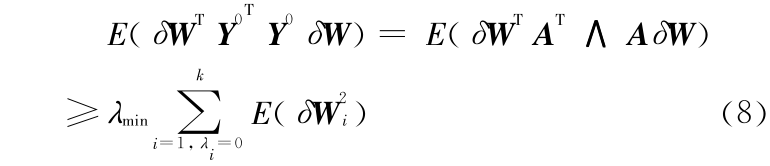
通过对 A 进行行初等变换（改变两行的位置），然后计算相应的式（2），将所得结果相加可得

其中，

结合式（1）可知

即，。

由上述定理可知，在邻域大小 k 已知情况下，离群点权值 W′ 主要由 3 个因素决定：a. 数据点之间距离 d 的大小；b. 邻域的影响，即 和秩 的大小；c. 真实值权值的‖ W ‖的大小。对于 a 要素可通过距离公式确定，b 要素可通过调整 和秩 两个值确定，c 要素直接由 LLE 算法可知。

《3.3 算法描述》

3.3 算法描述

输入：输入样本数据集 X ＝｛ x1 ，x2 ，…，xn ｝，xi ∈ RD ，邻域参数 k ；

输出：低维数据集中的离群点 y′i ；

步骤1 　对高维空间中的每个样本点 xi （i ＝ 1 ， 2 ，…，n），计算它和其他 n －1 个样本点之间的距离，根据距离的大小，选择前 K 个与 xi （ i ＝ 1 ，2 ，…， n）最近的点作为其邻近点，常采用欧氏距离来度量两个点之间的距离；

步骤2 　对每个 xi （ i ＝ 1 ，2 ，…， n），找到它的 K 个近邻点之后，计算该点和它的每个近邻点之间的权值 ，即最小化式（1）；

步骤 3 　对最小化所得的每一点的权值 min ∈（ w）组成一个权值矩阵，并对 W 进行约束限制；

步骤 4 　根据高维空间中的样本点 xi （ i ＝ 1 ，2 ，…， n）和它的近邻 xj （ j ＝ 1 ，2 ，…，K）之间的权值 来计算低维嵌入空间中的值 yi 和 yj ，即yi － ；

步骤 5 　根据式（3）重新选取邻域数 k ，并重复步骤 1 至步骤 4 ；

步骤 6 　根据距离公式改进降维后样本数据集中各点之间的距离，以利于发现样本数据集中的离群点；

步骤 7 　经过 LLE 算法降维，包括离群点的低维数据集是通过权值 W 计算而得，离群点权值的变化情况可依据判别定理，由式（4）得出；

步骤 8 　对从判别式中得到的离群点权值 W′，利用离群点的局部重建权值矩阵及近邻点的线性组合来表示出该离群点。

《4 算法的实现及其实验结果的评估》

4 算法的实现及其实验结果的评估

采用文章提出的算法对两个样本集进行实验，其中一个样本集是采用算法生成的曲线形柱面，另一个样本集来自于 UCI 标准数据库（http ：//www . ics . uci . edu／mlearn／MLRepository . htm1）。

整个实验运行在主频为 P42 .4 GHz 、内存为 512 MB 、80 GB 硬盘、操作系统为 Windows XP sp2 的主机上面。基于此环境，对整个算法进行相关性能测试。

第一个实验数据集为曲线形柱面（如图 1 所示），柱面上半部分由 30 个离群点组成，下半部分由 20 × 20 = 400 个采样点组成，数据点维数为三维，内在维数为两维。目的是将三维数据降为两维数据，并发现离群点。

《图 1》

图 1 曲线形柱面数据集

Fig .1 Data set formed by curve shape cylinder

实验中近邻点的个数 k 选择很重要，k 的取值太大，算法不能体现局部特性，而且降维效果显著变差，这是因为测试数据是比较弯曲的流形，容易发生短路现象。反之，算法不能保持样本点在低维空间中的拓扑结构。该处所选取的 k 值尽量使算法中最小化函数达到最小，因此根据式（3）选取k 为 9 。同时由于对降维后的数据点之间距离重新调整，使得降维后的样本数据集整体分布趋于均匀化，有利于近邻点计算，从而使数据集中的离群点更加突出。采用文章提出的算法，将三维的曲线形柱面降维至二维平面，并分离出离群点的效果如图 2 所示。

《图 2》

图 2 降维后分离出离群点的数据集

Fig .2 Outliers separated from data set after dimensionality reduction

第二个数据集为 MUSHROOM 数据集， MUSHROOM 数据集为 UCI 标准数据库之一。该数据集中训练样本为 210 个，测试样本为 8 124 个，样本的维数为 22 。表 1 给出了分别使用不同的基于距离的离群点检测算法和笔者提出的算法对 MUSHROOM 数据集进行学习和离群点分离的结果，其中提出算法在运行时需要指定不同参数的值，算法中的 k 值根据式（3）选取，其取值范围在 7 ~ 12 时效果较好，k 值的选取与测试错误率如图 3 所示。除此之外，还需根据式（4）调整降维后数据集中点之间的距离。笔者提出算法的测试分离离群点的错误率明显低于其他基于距离的离群点检测算法的测试错误率，而且该算法具有良好的特性，即 k 值的估计非常简单，且在一定范围内结果比较稳定。

《表 1》

表 1 不同算法对离群点的检测结果

Table 1 Experimental result of Outliers Detection Based on different algorithms

《图 3》

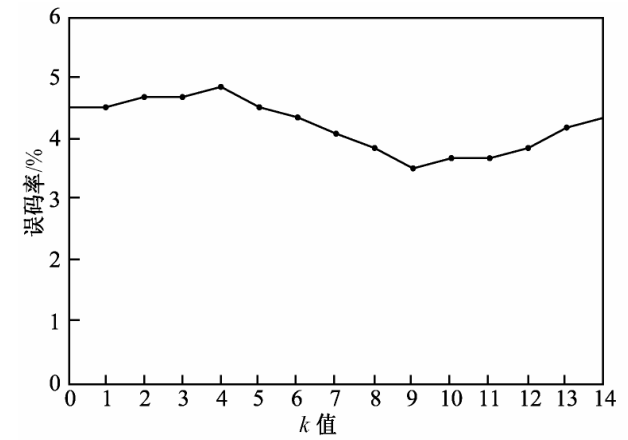
图 3 算法中 k 值对数据集中离群点检测错误率的影响

Fig .3 The effect of k value from algorithm on mistake rate detected in outliers from data set

实验表明该方法是正确的，为了更好地应用，应注意以下几个方面：

1）如果维数较高，离群点较多，计算时间增加，如离群点个数较少，运算时间明显加快；

2）可以使用增量技术，用户选择某个阈值，计算了一个结果后，不用全部从头开始计算两点距离，可以大大减少运行时间；

3）距离的选取非常重要，实验中采用改进的距离公式，可以根据挖掘数据的目标，将所感兴趣的离群数据值加权。

实验说明了笔者提出的算法既保证了得到的结果相当接近于全局最优解，又保证了能非常快速地得到结果。即使对于样本的个数为8 124 、维数为 22 这样的高维大样本，也能快速得到比较满意的结果。

《5 结语》

5 结语

在分析了传统的离群数据挖掘算法优点和缺点的基础上，针对非线性高维数据集中的离群点检测问题，提出一种基于流形学习的离群点检测算法。该算法利用 LLE 算法的思想寻找样本数据的内在嵌入分布，并通过邻域数选取和降维后数据点之间的距离调整，提高了数据集中离群点发现效率，根据离群点权值判别式进行权值数据判定，依据权值的大小标识出数据集中的离群点。特别是对于一些线性不可分的数据集，在运用传统离群点检测算法失败的情况下，笔者提出的算法仍然能取得良好的离群点检测效果。