Analysis of A Block Cipher Based on Chaos

Abstract

In this paper, it is pointed out that the block cipher proposed in “Design of Block Cipher substitution network on chaos” can be broken by attack with known plaintext and attack with ciphertext only, and the key of this cipher can be found by the divide-and-conquer attack with the encipher transformation. Furthermore, the mutual restriction between the successive values of the chaos sequences based on the Logistic mapping, and the property that the frontal values of the chaos sequences are not sensitive to the bits on the lower po-sitions of the initial value are also pointed out.

Content

《1 相关知识》

1 相关知识

开区间 (0, 1) 中的每个实数a都可表示为 $a = \sum_{i = 1}^{\infty} a_{i} 2^{- i}, a_{i} \in {0, 1}$ $a = \sum_{i = 1}^{\infty} a_{i} 2^{- i}, a_{i} \in {0, 1}$ , 其中∀t>1, a_t, a_t+1, a_t+2, …不全为1。称 $\sum_{i = 1}^{m}$ $\sum_{i = 1}^{m}$ 为a的m精度小数。显然, 每个m精度小数都与{0, 1}^m中的m维二元向量一一对应。为方便起见, 称 (a₁, a₂, …, a_n) 为a的高n位。

文献[1]利用混沌变换f (x) = 4x (1-x) , 0<x<1产生的混沌序列构造了一个分组密码算法, 并认为该密码算法具有很高的安全性, 其具体构造方法如下:

设密钥规模为m比特, $x_{0} = \sum_{i = 1}^{m} k_{i} 2^{- i}$ $x_{0} = \sum_{i = 1}^{m} k_{i} 2^{- i}$ 为密钥k= (k₁, k₂, …, k_m) 对应的m精度小数, ∀i≥1, 递归地定义x_i为4x_i-1 (1-x_i-1) 的m精度小数, 这样就得到一条混沌序列x₀, x₁, x₂, …; 将该序列中诸元素x_i换作n精度 (n≤m) 小数x′_i后又得到该混沌序列的一条截尾序列x′₀, x′₁, x′₂, …。将序列2ⁿx′₀, 2ⁿx′₁, 2ⁿx′₂, … 的前2ⁿ个不同的元素依出现的次序分别记为p (0) , p (1) , …, p (2ⁿ-1) , 则由m比特的密钥k就产生了一个2ⁿ元置换p。在加密时, 先将明文每2ⁿ个字符分为一组, 然后将 (a_{p (0)}, a_{p (1)}, …, a_{p (2ⁿ-1)}) 作为明文分组 (a₀, a₁, …, a_2ⁿ-1) 对应的密文。当然, 也可采取将该加密变换的逆变换作为加密变换的方式。究竟采取哪种加密方式, 文献[1]中没有明确交代, 但这对分析没有本质的影响。

《2 对基于混沌序列的分组密码算法的分析》

2 对基于混沌序列的分组密码算法的分析

容易看出, 该分组密码算法本质上是利用秘密密钥产生一个古典的移位密码, 因而是极其脆弱的。由于移位密码的破译问题早已解决, 移位密码既不能抵抗已知明文攻击, 也不能抵抗唯密文攻击, 因而该文提出的分组密码算法没有安全性可言。

这里做了一例已知明文攻击实验。设密钥规模为64比特, 密钥为f0f1 f0f1 f0f1 f0f1 (16进制表示, 下同) , 则它产生的64元置换p将0, 1, …, 63依次变换为:

《图1》

取加密变换为x_i→x_{p (i)}, 则明文

《图2》

在最后添加21个空格后可构成6个分组, 其中每两行构成一个明文分组, 其加密结果为:

《图3》

记A_{k, i}是第k个密文分组中出现第k明文分组中的第i个字母 (0≤i≤63) 的位置全体构成的集合, $A_{i} = \cap_{k = 1}^{t} A_{k, i}$ $A_{i} = \cap_{k = 1}^{t} A_{k, i}$ , 则当A₀, A₁, …, A₆₃都是单点集合时, 映射p就唯一确定了。实验表明: 对于64字符分组的加密算法, 只要利用3个分组 (即取t=3) 就能按上述方法唯一确定出映射p; 对于128字符分组的加密算法, 只要利用4个分组 (即取t=4) 就能按上述方法唯一确定出映射p。

由于对移位密码的唯密文攻击也有成熟的攻击方法, 这里不再多叙。此时, 借助明文的内在规律, 就可在仅知道密文的条件下对移位密码实现破译。

《3 混沌序列的内在规律》

3 混沌序列的内在规律

下面将要指出:混沌序列的截尾序列x′₀, x′₁, x′₂, …的相邻信号之间具有很强的相互制约关系, 而且初值x₀的低位比特对x′₀, x′₁, x′₂, …的前几个值几乎没有影响, 换句话说, x′₀, x′₁, x′₂, …的前几个值只与初值x₀的高位比特有关。借助这两个性质, 可以减少破译该分组密码所需的已知明文量或已知密文量, 并求出产生该移位变换的密钥k。

例如, 对于上面的攻击实验, 对于64字符分组的加密算法, 只要利用2个密文分组就可确定出p (0) , p (1) , …, p (63) 中除

$\begin{array}{l} p (1), p (7), p (12), p (15), p (19), p (28), \\ p (46), p (51), p (53), p (54), p (62) \end{array}$ $\begin{array}{l} p (1), p (7), p (12), p (15), p (19), p (28), \\ p (46), p (51), p (53), p (54), p (62) \end{array}$

以外的全部值; 借助x′_i与x′_i+1的相互制约性可直接假设出p (1) , p (7) , p (12) , 再借助后一个性质, 就可利用分割攻击方法求出密钥k, 从而完全确定出移位变换p。具体攻击方法将在介绍完攻击原理后再给予介绍。以下分别用 $\exists (x)$ $\exists (x)$ 和ceil (x) 表示不大于x的最大整数和不小于x的最小整数。

定理1 设x₀, x₁, x₂, … 是利用混沌变换f (x) =4x (1-x) , 0<x<1由m精度的初值x₀产生的m精度小数序列, x′_i是x_i的n精度小数, 则在x′_i给定时, x′_i+1至多有5种变化, 且2ⁿx′_i+1的可能取值范围是仅与x′_i有关的连续的整数。

证明设x_i=x′_i+a, 则0≤a<2^-n, 且由x_i是m精度的小数知0≤a≤2^-n-2^-m, 故有x′_i≤x_i≤x′_i+2^-n-2^-m。又由f (x) =1- (2x-1) ²知 $2^{n} x^{'}_{i + 1} = \exists (2^{n} f (x_{i})) = \exists (2^{n} - 2^{n} (2 x_{i} - 1)^{2})$ $2^{n} x^{'}_{i + 1} = \exists (2^{n} f (x_{i})) = \exists (2^{n} - 2^{n} (2 x_{i} - 1)^{2})$ 。

现借助x′_i≤x_i≤x′_i+2^-n-2^-m这个条件, 考查整数2ⁿx′_i+1的取值范围。

由于 $\frac{d}{d x} f (x) = - 4 (2 x - 1)$ $\frac{d}{d x} f (x) = - 4 (2 x - 1)$ , 故当0<x≤0.5时, f (x) 为增函数; 当0.5≤x<1时, f (x) 为减函数。下面分两种情况证明。

1) 如果x′i<0.5, 则由x′i是n精度小数知x′i≤0.5-2-n, 从而

$x^{'}_{i} \leq x_{i} \leq x^{'}_{i} + 2^{- n} - 2^{- m} \leq 0.5 - 2^{- m} 。$ $x^{'}_{i} \leq x_{i} \leq x^{'}_{i} + 2^{- n} - 2^{- m} \leq 0.5 - 2^{- m} 。$

再由0<x≤0.5时f (x) 为增函数知f (x′_i) ≤f (x_i) ≤f (x′_i+2^-n-2^-m) , 因而

$\begin{array}{l} \begin{array}{l} \exists (2^{n} f (x^{'}_{i})) \leq \exists (2^{n} f (x_{i})) \leq \\ \exists (2^{n} f (x^{'}_{i} + 2^{- n} - 2^{- m})), \\ 即 \\ \exists (2^{n} f (x^{'}_{i})) \leq 2^{n} x^{'}_{i + 1} \leq \end{array} \\ \exists (2^{n} f (x^{'}_{i} + 2^{- n} - 2^{- m})) 。 \end{array}$ $\begin{array}{l} \begin{array}{l} \exists (2^{n} f (x^{'}_{i})) \leq \exists (2^{n} f (x_{i})) \leq \\ \exists (2^{n} f (x^{'}_{i} + 2^{- n} - 2^{- m})), \\ 即 \\ \exists (2^{n} f (x^{'}_{i})) \leq 2^{n} x^{'}_{i + 1} \leq \end{array} \\ \exists (2^{n} f (x^{'}_{i} + 2^{- n} - 2^{- m})) 。 \end{array}$

由n<m知2^2-m-2^2-n<0, 令

$\begin{array}{l} g (x) = 2^{n} f (x + 2^{- n} - 2^{- m}) - 2^{n} f (x), \\ 则 \\ g (x) = \\ 2^{n} [(2^{2 - m} - 2^{2 - n}) (2 x - 1) - (2^{1 - m} - 2^{1 - n})^{2}] \end{array}$ $\begin{array}{l} g (x) = 2^{n} f (x + 2^{- n} - 2^{- m}) - 2^{n} f (x), \\ 则 \\ g (x) = \\ 2^{n} [(2^{2 - m} - 2^{2 - n}) (2 x - 1) - (2^{1 - m} - 2^{1 - n})^{2}] \end{array}$

是减函数, 因而

$\begin{array}{l} g (x^{'}_{i}) < g (0) = \\ 2^{n} [(2^{2 - n} - 2^{2 - m}) - (2^{1 - m} - 2^{1 - n})^{2}] < 4 。 \end{array}$ $\begin{array}{l} g (x^{'}_{i}) < g (0) = \\ 2^{n} [(2^{2 - n} - 2^{2 - m}) - (2^{1 - m} - 2^{1 - n})^{2}] < 4 。 \end{array}$

再记

$\begin{array}{l} 2^{n} f (x^{'}_{i} + 2^{- n} - 2^{- m}) = \\ 1 \exists (2^{n} f (x^{'}_{i} + 2^{- n} - 2^{- m})) + α, \\ 2^{n} f (x^{'}_{i}) = \exists (2^{n} f (x^{'}_{i})) + β, \end{array}$ $\begin{array}{l} 2^{n} f (x^{'}_{i} + 2^{- n} - 2^{- m}) = \\ 1 \exists (2^{n} f (x^{'}_{i} + 2^{- n} - 2^{- m})) + α, \\ 2^{n} f (x^{'}_{i}) = \exists (2^{n} f (x^{'}_{i})) + β, \end{array}$

则0≤α, β<1, 因而α-β<1, 从而2ⁿx′_i+1的可能取值个数为

$\begin{array}{l} \exists (2^{n} f (x^{'}_{i} + 2^{- n} - 2^{- m})) - \exists (2^{n} f (x^{'}_{i})) + 1 = \\ 2^{n} f (x^{'}_{i} + 2^{- n} - 2^{- m}) - 2^{n} f (x^{'}_{i}) + α - β + 1 < \\ 5 + α - β < 6 。 \end{array}$ $\begin{array}{l} \exists (2^{n} f (x^{'}_{i} + 2^{- n} - 2^{- m})) - \exists (2^{n} f (x^{'}_{i})) + 1 = \\ 2^{n} f (x^{'}_{i} + 2^{- n} - 2^{- m}) - 2^{n} f (x^{'}_{i}) + α - β + 1 < \\ 5 + α - β < 6 。 \end{array}$

2) 如果x′i≥0.5, 则有0.5≤x′i≤xi≤x′i+2-n-2-m。再由0<x≤0.5时f (x) 为减函数知f (x′i+2-n-2-m) ≤f (xi) ≤f (x′i) , 因而

$\begin{array}{l} \exists (2^{n}) f (x^{'}_{i} + 2^{- n} - 2^{- m})) \leq \\ \exists (2^{n}) f (x_{i})) \leq \exists (2^{n} f (x^{'}_{i})), \\ 即 \\ \exists (2^{n}) f (x^{'}_{i} + 2^{- n} - 2^{- m})) \leq \\ 2^{n} x^{'}_{i + 1} \leq \exists (2^{n} f (x^{'}_{i})) 。 \end{array}$ $\begin{array}{l} \exists (2^{n}) f (x^{'}_{i} + 2^{- n} - 2^{- m})) \leq \\ \exists (2^{n}) f (x_{i})) \leq \exists (2^{n} f (x^{'}_{i})), \\ 即 \\ \exists (2^{n}) f (x^{'}_{i} + 2^{- n} - 2^{- m})) \leq \\ 2^{n} x^{'}_{i + 1} \leq \exists (2^{n} f (x^{'}_{i})) 。 \end{array}$

由n<m知2^2-m-2^2-n<0。

令

$\begin{array}{l} g (x) = 2^{n} f (x) - 2^{n} f (x + 2^{- n} - 2^{- m}), \\ 则 \\ g (x) = \\ 2^{n} [(2^{2 - n} - 2^{2 - m}) (2 x - 1) + (2^{1 - n} - 2^{1 - m})^{2}] \end{array}$ $\begin{array}{l} g (x) = 2^{n} f (x) - 2^{n} f (x + 2^{- n} - 2^{- m}), \\ 则 \\ g (x) = \\ 2^{n} [(2^{2 - n} - 2^{2 - m}) (2 x - 1) + (2^{1 - n} - 2^{1 - m})^{2}] \end{array}$

是增函数, 故由x′_i≤1-2^-n知

$\begin{array}{l} g (x^{'}_{i}) \leq \\ g (1 - 2^{n}) = 4 - 2^{2 - n} - (1 - 2^{- m}) 2^{2 + n - m} < 4, \end{array}$ $\begin{array}{l} g (x^{'}_{i}) \leq \\ g (1 - 2^{n}) = 4 - 2^{2 - n} - (1 - 2^{- m}) 2^{2 + n - m} < 4, \end{array}$

从而类似x′_i<0.5的情形可证:

$\begin{array}{l} \exists (2^{n} f (x^{'}_{i})) - \\ \exists (2^{n} f (x^{'}_{i} + 2^{- n} - 2^{- m})) + 1 < 6, \end{array}$ $\begin{array}{l} \exists (2^{n} f (x^{'}_{i})) - \\ \exists (2^{n} f (x^{'}_{i} + 2^{- n} - 2^{- m})) + 1 < 6, \end{array}$

这说明x′_i+1至多有5种变化。显然x′_i+1这些可能的取值都是连续的。

实验结果与定理1完全吻合。当定理1中的m=64且n=6时, x′_i的后继x′_i+1的取值个数是1, 2, 3, 4, 5的分别有8, 16, 16, 16和8 个。

定理2 设x₀, x₁, x₂, … 是利用混沌变换f (x) =4x (1-x) , 0<x<1由m精度的初值x₀产生的m精度小数序列, x′_i是x_i的n精度小数, 则在x′_i+1给定时, 如果x′_i+1=2ⁿ-1, 则x′_i至多有 $\exists (2^{\frac{n}{2} - 1}) + c e i l$ $\exists (2^{\frac{n}{2} - 1}) + c e i l$ $(2^{\frac{n}{2} - 1}) + 1$ $(2^{\frac{n}{2} - 1}) + 1$ 种变化, 否则x′_i至多有 $\exists (2^{\frac{n + 1}{2}}) - 2^{\frac{n}{2}}) + 4$ $\exists (2^{\frac{n + 1}{2}}) - 2^{\frac{n}{2}}) + 4$ 种变化。此外, x′_i的取值范围是仅与x′_i有关的连续的整数。

证明由f (x) =1- (2x-1) ²知

$2^{n} x^{'}_{i + 1} = \exists (2^{n} f (x_{i})) = \exists (2^{n} - 2^{n} (2 x_{i} - 1)^{2})$ $2^{n} x^{'}_{i + 1} = \exists (2^{n} f (x_{i})) = \exists (2^{n} - 2^{n} (2 x_{i} - 1)^{2})$ 。

由于f (x_i) =1- (2x_i-1) ²是精度为2m的小数, 故有

x′_i+1≤1- (2x_i-1) ²≤x′_i+1+2^-n-2^-2m,

从而

2^2n-2+2^2n-2m-2-2^n-2 (2ⁿx′_i+1+1) ≤

(2ⁿx_i-2^n-1) ²≤2^2n-2-2^2n-2x′_i+1,

故有

$\frac{1}{2} \sqrt{2^{2 n} + 2^{2 n - 2 m} - 2^{n} (2^{n} x^{'}_{i + 1} + 1)} \leq$ $\frac{1}{2} \sqrt{2^{2 n} + 2^{2 n - 2 m} - 2^{n} (2^{n} x^{'}_{i + 1} + 1)} \leq$

2ⁿx_i-2^n-1 $\leq \frac{1}{2} \sqrt{2^{2 n} - 2^{2 n} x^{'}_{i + 1}},$ $\leq \frac{1}{2} \sqrt{2^{2 n} - 2^{2 n} x^{'}_{i + 1}},$

因而

$\begin{array}{l} 2^{n - 1} + \frac{1}{2} \sqrt{2^{2 n} + 2^{2 n - 2 m} - 2^{n} (2^{n} x^{'}_{i + 1} + 1)} \leq \\ 2^{n} x_{i} \leq 2^{n - 1} + \frac{1}{2} \sqrt{2^{2 n} - 2^{2 n} x^{'}_{i + 1}}, \end{array}$ $\begin{array}{l} 2^{n - 1} + \frac{1}{2} \sqrt{2^{2 n} + 2^{2 n - 2 m} - 2^{n} (2^{n} x^{'}_{i + 1} + 1)} \leq \\ 2^{n} x_{i} \leq 2^{n - 1} + \frac{1}{2} \sqrt{2^{2 n} - 2^{2 n} x^{'}_{i + 1}}, \end{array}$

或者

$\begin{array}{l} 2^{n - 1} - \frac{1}{2} \sqrt{2^{2 n} - 2^{2 n} x^{'}_{i + 1}} \leq \\ 2^{n} x_{i} \leq 2^{n - 1} - \frac{1}{2} \sqrt{2^{2 n} + 2^{2 n - 2 m} - 2^{n} (2^{n} x^{'}_{i + 1} + 1)}, \end{array}$ $\begin{array}{l} 2^{n - 1} - \frac{1}{2} \sqrt{2^{2 n} - 2^{2 n} x^{'}_{i + 1}} \leq \\ 2^{n} x_{i} \leq 2^{n - 1} - \frac{1}{2} \sqrt{2^{2 n} + 2^{2 n - 2 m} - 2^{n} (2^{n} x^{'}_{i + 1} + 1)}, \end{array}$

故2ⁿx′_i的个数为

$\begin{array}{l} Ν = \exists (2^{n - 1} + \frac{1}{2} \sqrt{2^{2 n} - 2^{2 n} x^{'}_{i + 1}}) - \\ \exists (2^{n - 1} + \frac{1}{2} \sqrt{2^{2 n} + 2^{2 n - 2 m} - 2^{n} (2^{n} x^{'}_{i + 1} + 1)}) + 1 + \end{array}$ $\begin{array}{l} Ν = \exists (2^{n - 1} + \frac{1}{2} \sqrt{2^{2 n} - 2^{2 n} x^{'}_{i + 1}}) - \\ \exists (2^{n - 1} + \frac{1}{2} \sqrt{2^{2 n} + 2^{2 n - 2 m} - 2^{n} (2^{n} x^{'}_{i + 1} + 1)}) + 1 + \end{array}$

E $(2^{n - 1} - \frac{1}{2} \sqrt{2^{2 n} + 2^{2 n - 2 m} - 2^{n} (2^{n} x^{'}_{i + 1} + 1)}) -$ $(2^{n - 1} - \frac{1}{2} \sqrt{2^{2 n} + 2^{2 n - 2 m} - 2^{n} (2^{n} x^{'}_{i + 1} + 1)}) -$

$\begin{array}{l} E (2^{n - 1} - \frac{1}{2} \sqrt{2^{2 n} - 2^{2 n} x^{'}_{i + 1}}) + 1 = \\ \exists (\frac{1}{2} \sqrt{2^{2 n} - 2^{2 n} x^{'}_{i + 1}}) + c e i l (\frac{1}{2} \sqrt{2^{2 n} - 2^{2 n} x^{'}_{i + 1}}) - \\ \exists (\frac{1}{2} \sqrt{2^{2 n} + 2^{2 n - 2 m} - 2^{2 n} x^{'}_{i + 1} - 2^{n}}) - \\ c e i l (\frac{1}{2} \sqrt{2^{2 n} + 2^{2 n - 2 m} - 2^{2 n} x^{'}_{i + 1} - 2^{n}}) + 2 。 \end{array}$ $\begin{array}{l} E (2^{n - 1} - \frac{1}{2} \sqrt{2^{2 n} - 2^{2 n} x^{'}_{i + 1}}) + 1 = \\ \exists (\frac{1}{2} \sqrt{2^{2 n} - 2^{2 n} x^{'}_{i + 1}}) + c e i l (\frac{1}{2} \sqrt{2^{2 n} - 2^{2 n} x^{'}_{i + 1}}) - \\ \exists (\frac{1}{2} \sqrt{2^{2 n} + 2^{2 n - 2 m} - 2^{2 n} x^{'}_{i + 1} - 2^{n}}) - \\ c e i l (\frac{1}{2} \sqrt{2^{2 n} + 2^{2 n - 2 m} - 2^{2 n} x^{'}_{i + 1} - 2^{n}}) + 2 。 \end{array}$

当2ⁿx′_i+1=2ⁿ-1时,

$\begin{array}{l} Ν = \exists (2^{\frac{n}{2} - 1}) + c e i l (2^{\frac{n}{2} - 1}) - \\ \exists (2^{n - m - 1}) - c e i l (2^{n - m - 1}) + 2 = \\ \exists (2^{\frac{n}{2} - 1}) + c e i l (2^{\frac{n}{2} - 1}) + 1 。 \end{array}$ $\begin{array}{l} Ν = \exists (2^{\frac{n}{2} - 1}) + c e i l (2^{\frac{n}{2} - 1}) - \\ \exists (2^{n - m - 1}) - c e i l (2^{n - m - 1}) + 2 = \\ \exists (2^{\frac{n}{2} - 1}) + c e i l (2^{\frac{n}{2} - 1}) + 1 。 \end{array}$

一般地, 令

$\begin{array}{l} g (x) = \frac{1}{2} \sqrt{2^{2 n} - 2^{n} x} - \\ \frac{1}{2} \sqrt{2^{2 n} + 2^{2 n - 2 m} - 2^{n} (x + 1)}, \end{array}$ $\begin{array}{l} g (x) = \frac{1}{2} \sqrt{2^{2 n} - 2^{n} x} - \\ \frac{1}{2} \sqrt{2^{2 n} + 2^{2 n - 2 m} - 2^{n} (x + 1)}, \end{array}$

则g (x) 是严格增函数, 故当2ⁿx′_i+1≤2ⁿ-2时, 有

$\begin{array}{l} g (2^{n} x^{'}_{i + 1}) \leq g (2^{n} - 2) = \\ 2^{\frac{n - 1}{2}} - \sqrt{2^{2 n - 2 m - 2} + 2^{n - 2}} < 2^{\frac{n - 1}{2}} - 2^{\frac{n}{2} - 1} 。 \end{array}$ $\begin{array}{l} g (2^{n} x^{'}_{i + 1}) \leq g (2^{n} - 2) = \\ 2^{\frac{n - 1}{2}} - \sqrt{2^{2 n - 2 m - 2} + 2^{n - 2}} < 2^{\frac{n - 1}{2}} - 2^{\frac{n}{2} - 1} 。 \end{array}$

令

$\exists (\frac{1}{2} \sqrt{2^{2 n} - 2^{n} x^{'}_{i + 1}}) = \frac{1}{2} \sqrt{2^{2 n} - 2^{n} x^{'}_{i + 1}} - α,$ $\exists (\frac{1}{2} \sqrt{2^{2 n} - 2^{n} x^{'}_{i + 1}}) = \frac{1}{2} \sqrt{2^{2 n} - 2^{n} x^{'}_{i + 1}} - α,$

$\begin{array}{l} c e i l (\frac{1}{2} \sqrt{2^{2 n} - 2^{n} x^{'}_{i + 1}}) = \frac{1}{2} \sqrt{2^{2 n} - 2^{n} x^{'}_{i + 1}} + α^{'}, \\ \exists (\frac{1}{2} \sqrt{2^{2 n} + 2^{2 n - 2 m} - 2^{n} x^{'}_{i + 1} - 2^{n}}) = \\ \frac{1}{2} \sqrt{2^{2 n} + 2^{2 n - 2 m} - 2^{n} x^{'}_{i + 1} - 2^{n}} - β, \end{array}$ $\begin{array}{l} c e i l (\frac{1}{2} \sqrt{2^{2 n} - 2^{n} x^{'}_{i + 1}}) = \frac{1}{2} \sqrt{2^{2 n} - 2^{n} x^{'}_{i + 1}} + α^{'}, \\ \exists (\frac{1}{2} \sqrt{2^{2 n} + 2^{2 n - 2 m} - 2^{n} x^{'}_{i + 1} - 2^{n}}) = \\ \frac{1}{2} \sqrt{2^{2 n} + 2^{2 n - 2 m} - 2^{n} x^{'}_{i + 1} - 2^{n}} - β, \end{array}$

$\begin{array}{l} c e i l (\frac{1}{2} \sqrt{2^{2 n} + 2^{2 n - 2 m} - 2^{n} x^{'}_{i + 1} - 2^{n}}) = \\ \frac{1}{2} \sqrt{2^{2 n} + 2^{2 n - 2 m} - 2^{n} x^{'}_{i + 1} - 2^{n}} + β^{'}, \end{array}$ $\begin{array}{l} c e i l (\frac{1}{2} \sqrt{2^{2 n} + 2^{2 n - 2 m} - 2^{n} x^{'}_{i + 1} - 2^{n}}) = \\ \frac{1}{2} \sqrt{2^{2 n} + 2^{2 n - 2 m} - 2^{n} x^{'}_{i + 1} - 2^{n}} + β^{'}, \end{array}$

则0≤α, α′, β, β′<1, 于是α′-α<1, β-β′<1, 故由2ⁿx′_i+1≤2ⁿ-2知

$\begin{array}{l} Ν = \frac{1}{2} \sqrt{2^{2 n} - 2^{2 n} x^{'}_{i + 1}} - α + \frac{1}{2} \sqrt{2^{2 n} - 2^{2 n} x^{'}_{i + 1}} + \\ α^{'} - [\frac{1}{2} \sqrt{2^{2 n} + 2^{2 n - 2 m} - 2^{2 n} x^{'}_{i + 1} - 2^{n}} - β] - \\ [\frac{1}{2} \sqrt{2^{2 n} + 2^{2 n - 2 m} - 2^{2 n} x^{'}_{i + 1} - 2^{n}} + β^{'}] + 2 = \\ 2 g (2^{n} x^{'}_{i + 1}) + 2 + (α^{'} - α) + (β - β^{'}) < \\ 2 g (2^{n} - 2) + 4 = 2^{\frac{n + 1}{2}} - 2^{\frac{n}{2}} + 4 。 \\ 故有 \\ Ν \leq \exists (2 g (2^{n} - 2) + 4) = \exists (2^{\frac{n + 1}{2}} - 2^{\frac{n}{2}}) + 4 。 \end{array}$ $\begin{array}{l} Ν = \frac{1}{2} \sqrt{2^{2 n} - 2^{2 n} x^{'}_{i + 1}} - α + \frac{1}{2} \sqrt{2^{2 n} - 2^{2 n} x^{'}_{i + 1}} + \\ α^{'} - [\frac{1}{2} \sqrt{2^{2 n} + 2^{2 n - 2 m} - 2^{2 n} x^{'}_{i + 1} - 2^{n}} - β] - \\ [\frac{1}{2} \sqrt{2^{2 n} + 2^{2 n - 2 m} - 2^{2 n} x^{'}_{i + 1} - 2^{n}} + β^{'}] + 2 = \\ 2 g (2^{n} x^{'}_{i + 1}) + 2 + (α^{'} - α) + (β - β^{'}) < \\ 2 g (2^{n} - 2) + 4 = 2^{\frac{n + 1}{2}} - 2^{\frac{n}{2}} + 4 。 \\ 故有 \\ Ν \leq \exists (2 g (2^{n} - 2) + 4) = \exists (2^{\frac{n + 1}{2}} - 2^{\frac{n}{2}}) + 4 。 \end{array}$

即2ⁿx′_i至多有 $\exists (2^{\frac{n + 1}{2}} - 2^{\frac{n}{2}}) + 4$ $\exists (2^{\frac{n + 1}{2}} - 2^{\frac{n}{2}}) + 4$ 种可能值, 显然这些可能值都是连续的整数。

例如, 如果n=6, 则当2ⁿx′_i+1=63时, 2ⁿx′_i至多有

$Ν = \exists (2^{\frac{6}{2} - 1}) + c e i l$ $Ν = \exists (2^{\frac{6}{2} - 1}) + c e i l$ $(2^{\frac{6}{2} - 1}) + 1 = 9$ $(2^{\frac{6}{2} - 1}) + 1 = 9$

种变化; 当2ⁿx′_i+1≤62时, 2ⁿx′_i至多有 $\exists (2^{\frac{6 + 1}{2}} - 2^{\frac{6}{2}}) + 4 = 7$ $\exists (2^{\frac{6 + 1}{2}} - 2^{\frac{6}{2}}) + 4 = 7$ 种变化。实际的值比7都小, 而且基本上都是2和4。

定理2再次说明3ⁿx′_i与2ⁿx′_i+1之间有很强的相互制约关系。下面指出混沌序列x′₀, x′₁, x′₂, …的另一个弱点。

定理3 设f (x) =4x (1-x) , 0<x<1, 0<ε<1, 则|f (x+ε) -f (x) |≤4ε (1+ε) 。

证明由f (x+ε) -f (x) =-4ε (2x+ε-1) 即知|f (x+ε) -f (x) ≤4ε (1+ε) 。

推论设ε₀=ε为m精度小数 $ε_{k + 1} = 2^{- m} \exists (2^{m} ε_{k} (1 + ε_{k})), k \geq 0$ $ε_{k + 1} = 2^{- m} \exists (2^{m} ε_{k} (1 + ε_{k})), k \geq 0$ 又设x′_k和y′_k分别为初值x₀和y₀对应的混沌序列的截尾序列的值, 且y₀-x₀=ε, 则有

$| y^{'}_{k} - x^{'}_{k} | \leq 4^{k} ε_{k + 1}$ $| y^{'}_{k} - x^{'}_{k} | \leq 4^{k} ε_{k + 1}$ 。

证明由于f (x) 和f (x+ε) 都是m精度的小数, 故定理3的结论还可进一步精确为

$| f (x + ε) - f (x) | \leq 2^{2 - m} \exists (2^{m} ε (1 + ε)),$ $| f (x + ε) - f (x) | \leq 2^{2 - m} \exists (2^{m} ε (1 + ε)),$

由此利用归纳法就可证得本推论。

设g (x) =x+δ, 0≤x, δ<1, 则g (x) ≥1的概率为δ, 故定理3及其推论说明, 当ε很小时, 初值x₀中低位比特的变化对混沌序列的截尾序列x′₀, x′₁, x′₂, …的开头几个信号几乎没有影响, 也就是说x′₀, x′₁, x′₂, …的前几个值只与初值x₀的高位比特有关。

例如, 取m=128, n=7, ε=2^-64, 则ε_k≈2^2k-64, 由于当初值x₀的低64位变化时, 必有ε<2^-64, 故此时前20个信号都不改变的概率不小于 $1 - \prod_{k = 1}^{20} (1 - 2^{2 k - 64}) \approx 1$ $1 - \prod_{k = 1}^{20} (1 - 2^{2 k - 64}) \approx 1$ , 即前20个信号几乎不会改变, 实验也证实了这个结果。

这个特性为利用截尾序列x′₀, x′₁, x′₂, …对其初值x₀实施分割攻击奠定了基础。

《4 对基于混沌序列的分组密码算法的密钥的分割攻击》

4 对基于混沌序列的分组密码算法的密钥的分割攻击

《4.1 分割攻击算法》

4.1 分割攻击算法

以m=64为例做了一例实验, 实际的密钥k取为f0f1 f0f1 f0f1 f0f1。实验密钥k′的高16位至低16位依次记为k₁, k₂, k₃, k₄, 采取对k₁, k₂, k₃, k₄逐个穷举的方法对正确密钥k实施分割攻击。记y′₀, y′₁, y′₂, …为以y为初值产生的截尾序列。具体算法如下:

Step 1 记n₁=3, n₂=19, n₃=36, n₄=640, m₁=2¹⁰, m₂=m₃=m₄=2¹⁶。令k₁=0, t=1。

Step 2 执行 $k^{'} \leftarrow x^{'}_{0} + \sum_{i = 1}^{t} k_{i} 2^{- 16 i}$ $k^{'} \leftarrow x^{'}_{0} + \sum_{i = 1}^{t} k_{i} 2^{- 16 i}$ , 并检查以k′为初值产生的截尾序列片段y′₀, y′₁, …, y′_{n_t}是否与x′₀, x′₁, x′₂, …的相应值一致。

如果全部一致, 则在t=4时将k′作为候选密钥输出, 算法终止; 在t<4时将t增1后, k_t=1令并返回Step 2。如果不全一致, 则执行Step 3。

Step 3 将k_t增1后判断k_t=m_t是否成立。当k_t≠m_t时返回执行Step 2, 当k_t=m_t时判断t是否为1。如果t=1, 则报告算法失败, 终止; 如果t≠1, 则令k_t=0, 并将t减1后返回执行Step 3。

《图4》

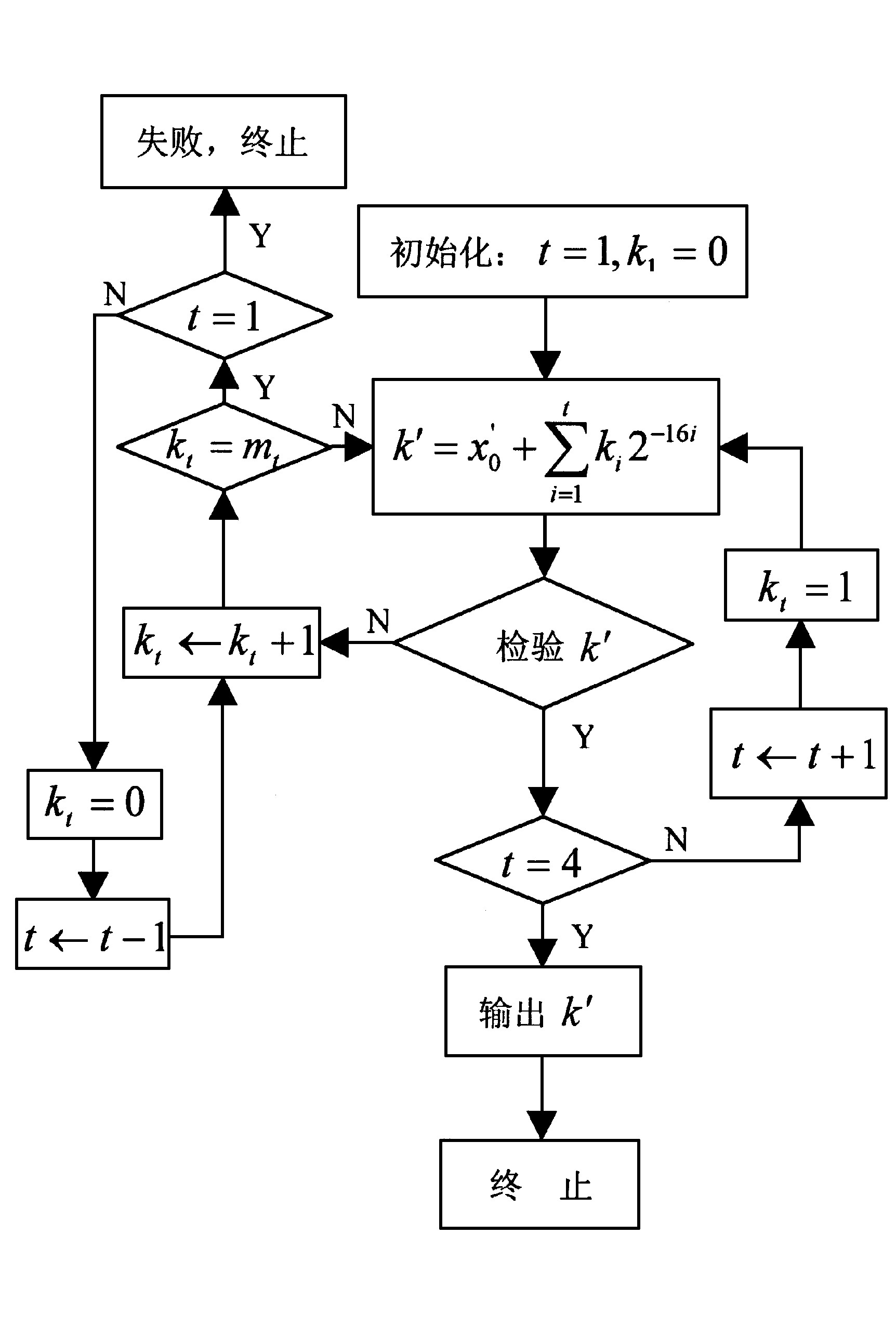
图1 分割攻击算法流程图

Fig.1 The flow diagram of the algorithm of divide-and-conquer attack

几点说明:1) 由于x′₀就是初值x₀的高6位比特, 因而密钥k=x₀的高6比特可直接由x′₀获得;

2) 实验表明, 在上述算法中, 如果限定t=1, 则通过Step 2的k₁的范围是从f0ae至 f102, 共85个;如果限定t≤2, 则通过Step 2的 (k₁, k₂) 的范围是从f0f1 f0d4至f0f1 f119, 共70个;如果限定t≤3, 则通过Step 2的 (k₁, k₂, k₃) 的范围是从 f0f1 f0f1 f0ed至f0f1 f0f1 f0ff, 共19个;通过全部检验的只有正确密钥。

3) 在不知序列x′₀, x′₁, x′₂, …但已知其产生的移位变换p的条件下, 将上述算法适当修改, 仍可求出正确密钥。这时, 只需将Step 2中“检查y′₀, y′₁, …, y′_{n_i}是否与x′₀, x′₁, x′₂, …的相应值一致”改为“检查y′₀, y′₁, …, y′_{n_i}产生的不同值p′ (0) , p′ (1) , …, p′ (s) 是否与p (0) , p (1) , …, p (s) 的相应值一致”即可。实验表明, 此时仍可唯一求出正确密钥。

4) 即使移位变换p的值有几个未知, 在对攻击算法做适当改动的条件下, 仍可求出正确密钥。实验表明, 对于前面提到的对64字符分组的分组密码的已知明文攻击, 在仅知两个分组的已知明文的条件下, 仍然可以唯一求出正确密钥。

《4.2 分割攻击算法的进一步完善》

4.2 分割攻击算法的进一步完善

上述分割攻击算法中n_i的选取需根据大量的实验确定。当n_i选取得太小时, 会造成k_i的候选量太多, 因而增加算法的计算复杂性;当n_i选取得太大时, 又会漏掉正确的k_i, 为此, 可利用混沌序列可能初值的分布特性进一步完善对密钥的分割攻击方案。

定理4 设f (x) =4x (1-x) , 则开区间 (0, 1) 中使得 $a \leq \exists (2^{n} f (z)) \leq b$ $a \leq \exists (2^{n} f (z)) \leq b$ 的点z形成两个分别位于 (0, 0.5]和[0.5, 1) 的闭区间。

证明由 $\exists (x)$ $\exists (x)$ 是增函数, 以及f (x) 在 (0, 0.5]和[0.5, 1) 内分别递增和递减知 $\exists (2^{n} f (z))$ $\exists (2^{n} f (z))$ 在 (0, 0.5]和[0.5, 1) 内连续且分别递增和递减, 故由闭区间关于连续的单调函数的逆像仍是闭区间即知本定理成立。

推论1 设x′₀, x′₁, x′₂, …是前面定义的序列, 则使得x′_i=a_i对0≤i≤k都成立的初值x₀对应的2^mx₀构成[0, 2^m]中的一个连续整数片段。

证明由定理4即知推论1在k=1时成立。设推论1对k-1成立, 则使x′_i=a_i对1≤i≤k都成立的m精度小数x₁全体形成一个连续片段[c, d]。由定理4知, 使得c≤x₁≤d成立的m精度小数x₀在 (0, 0.5]和[0.5, 1) 中各形成一个连续片段, 因而它们与 ${x \in (0, 1) ∶ \exists (2^{n} x) = x^{'}_{0}}$ ${x \in (0, 1) ∶ \exists (2^{n} x) = x^{'}_{0}}$ 的交集构成一个m精度小数的连续片段。

推论2 设x′₀, x′₁, x′₂, …是前面定义的序列, p (0) , p (1) , …, p (k) 是由序列{x′_i}^∞_i=0产生的Z/ (2ⁿ) 中的前k+1个互不相同数, k<2ⁿ, 记p′ (0) , p′ (1) , …, p′ (k) 是由初值y₀产生的序列{y′_i}^∞_i=0构造的Z/ (2ⁿ) 中的前k+1的互不相同数, 则使得p′ (i) =p (i) 对0≤i≤k都成立的所有初值y₀对应的2^my₀构成[0, 2^m]中的若干个连续的整数片段。

证明设由y′₀, y′₁, y′₂, …, y′_t可造出p (0) , p (1) , …, p (k) , 则混沌序列产生的前t+1个n精度小数是y′₀, y′₁, y′₂, …, y′_t的初值y₀全体构成一个连续片段。又因可造出p (0) , p (1) , …, p (k) 的y′₀, y′₁, y′₂, …, y′_t有多种可能, 因而能产生p (0) , p (1) , …, p (k) 的初值全体将形成多个连续片段。

由此可知, 搜索混沌序列的初值所得的解一般是连续的。如果记录下通过分割攻击算法第i+1步的k_i所在连续整数片段的端点及该片段中点的个数, 则当因某个n_i选取太大而漏掉正确的k_i时, 就可在k_i所在的连续整数片段向外偏移几个点搜索k_i。一般来说, 从个数较少的那些连续整数片段向外偏移来搜索k_i时成功率较大。

《5 结语》

5 结语

作者分析了“基于混沌的分组密码置换网络的设计”一文设计的分组密码的不安全性, 并给出了相应的攻击算法。混沌序列的截尾序列的相邻值之间具有很强的相互制约性, 且前若干值主要由初值的高位比特决定。一个安全的分组密码算法不仅要有足够的分组规模和密钥规模, 而且还必须满足混乱和扩散等设计标准, 所设计的算法必须能够经得住选择明文等攻击方法的考验。在将混沌变换应用于密码领域时, 必须设法克服混沌变换的自身弱点。

Show More